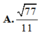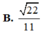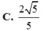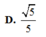Chọn A
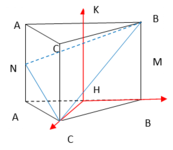
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
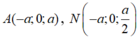
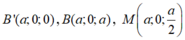
Xét mặt phẳng (BC'N) có
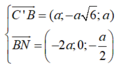
![]()
Phương trình (BC'N) là:
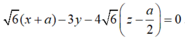
Khoảng cách từ M đến (BC'N) là:
![]()
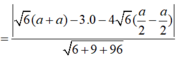

Chọn A

Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
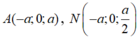
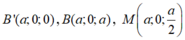
Xét mặt phẳng (BC'N) có
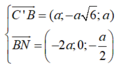
![]()
Phương trình (BC'N) là:
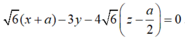
Khoảng cách từ M đến (BC'N) là:
![]()
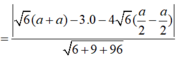

Cho lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông cân tại A, AB = AC = 2a, AA' = 3a. Gọi M là trung điểm AC, N là trung điểm BC. Khoảng cách từ điểm C đến mặt phẳng (A'MN)
A. 2 a 10
B. 3 a 10
C. 6 a 10
D. a 10
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=a, AA'= 2a. Gọi M là trung điểm của đoạn thẳng A'C', I là giao điểm của AM và AC'. Tính khoảng cách từ điểm A đến mặt phẳng (IBC).
A . 2 5 a 5
B . 5 a 5
C . 2 3 a 5
D . 3 a 5
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=AA'=a (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng BC' và mặt phẳng (ABB'A').
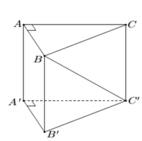
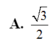
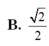
![]()
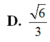
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC=2a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm H của cạnh AB và AA' = a 2 . Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
A. V = a 3 6 6
B. V = a 3 3
C. V = a 3 6 2
D. V = a 3 2
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm O của cạnh AB. Số đo của góc giữa đường thẳng AA' và mặt phẳng ( A ' B ' C ' ) bằng 60 0 . Gọi I là trung điểm của cạnh B’C’. Khoảng cách giữa hai đường thẳng CI và AB’ bằng
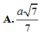
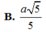
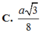
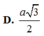
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân đỉnh A , AB = 2a, AA' = 2a, hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của cạnh BC . Thể tích của khối lăng trụ ABC.A'B'C' bằng
A. 4 a 3 2
B. 2 a 3 2
C. a 3 14 4
D. 2 a 3 2 3
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên AA'=a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B' C là:
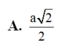
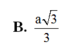
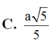
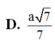
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, BAC = 30 ° , AB = a 3 , AA' = a. Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'.
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A lên mặt phẳng ( A ' B ' C ' ) là trung điểm H của A’B’. Gọi M, N lần lượt là trung điểm của A A ' , B ' C ' . Biết rằng AH = 2a và α là số đo của góc giữa đường thẳng MN và mặt phẳng ( A C ' H ) . Khi đó cos α bằng