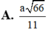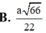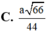Question

Cho hình hóp S.ABCD, có đáy ABCD là hình thang vuông tại A và D. Gọi E là trung điểm của AB. Biết AB = 2a, AD = DC = a, đồng thời SA vuông góc AB, SA vuông góc AD và SA = \(\dfrac{2a\sqrt{3}}{3}\). Khi đó

Các mệnh đề sau đúng hay sai?

a) (SB, DC ) = \(\widehat{SBA}\)

b) \(tan\widehat{SBA}=\dfrac{\sqrt{3}}{2}\)

c) DE song song BC

d) (SD,BC) xấp xỉ \(52,42^o\)

Answer 1

a, Đ 

Vì DC // AB (do ABCD là hình thang), góc giữa SB và DC bằng góc giữa SB và AB, tức là \(\widehat{SBA}\)

b, S

\(\Delta\)SAB \(\perp\) A, ta có

\(tan\widehat{SBA}\) = \(\dfrac{SA}{AB}\) = \(\dfrac{\text{2a√3}}{\dfrac{3}{2a}}\) =\(\dfrac{\text{ √3}}{3}\)

c, S

Gọi F là TĐ của AB. Khi đó, \(AF = FB = a\).

 Xét hình thang ABCD, ta có:

\(AD = DC = a, AB = 2a.\)

Suy ra, \(\text{AF = AD = DC = a.}\)

Tứ giác AFCD là hình vuông.

 Ta có: \(AE = EB = a, AF = AD = a.\)

 Xét \(\Delta\) ADE và \(\Delta\) CBF, ta thấy chúng không đồng dạng, do đó DE không // BC.

d, S

≈ 74,99°