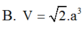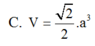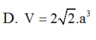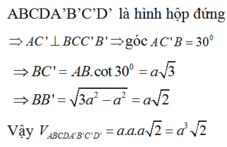Các câu hỏi tương tự
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) một góc 30
°
. Tính thể tích của khối hộp ABCD.A’B’C’D’ bằng
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) một góc 30 ° . Tính thể tích của khối hộp ABCD.A’B’C’D’ bằng
![]()
![]()
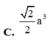
![]()
Cho hình hộp đứng
A
B
C
D
.
A
1
B
1
C
1
D
1
có đáy ABCD là hình vuông cạnh a, đường thẳng
D
B
1
tạo với mặt phẳng
(
B
C
C
1
B
1
)
góc...
Đọc tiếp
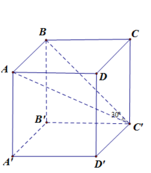
Cho hình hộp đứng A B C D . A 1 B 1 C 1 D 1 có đáy ABCD là hình vuông cạnh a, đường thẳng D B 1 tạo với mặt phẳng ( B C C 1 B 1 ) góc 30 0 . Tính thể tích khối hộp A B C D . A 1 B 1 C 1 D 1 .
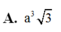

![]()
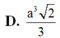
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và
B
D
C
⏜
60
0
, AB’ hợp với đáy (ABCD) một góc
30
0
. Thể tích của khối hộp là
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và B D C ⏜ = 60 0 , AB’ hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
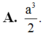
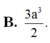
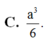
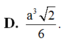
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,
BCD
^
120° và AA 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’. A. V 12
a
3
B. V 3
a
3
C. V 9
a
3
D. V 6
a
3
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD ^ = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh bên AA3a và đường chéo AC5a. Thể tích V của hình hộp đứng ABCD.A’B’C’D’ bằng bao nhiêu?
Đọc tiếp
Hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh bên AA'=3a và đường chéo AC'=5a. Thể tích V của hình hộp đứng ABCD.A’B’C’D’ bằng bao nhiêu?
![]()
![]()
![]()
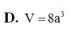
Cho hình hộp đứng
A
B
C
D
.
A
1
B
1
C
1
D
1
có đáy ABCD là hình vuông cạnh 2a, đường thẳng
D
B
1...
Đọc tiếp
Cho hình hộp đứng A B C D . A 1 B 1 C 1 D 1 có đáy ABCD là hình vuông cạnh 2a, đường thẳng D B 1 tạo với mặt phẳng ( B C B 1 C 1 ) góc 30 o . Tính thể tích khối hộp A B C D . A 1 B 1 C 1 D 1
A. a 3 3
B. a 3 2 3
C. 8 a 3 2
D. a 3
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 2a, có đáy là hình vuông và cạnh bên tạo với mặt phẳng đáy khối hộp một góc bằng
60
o
Thể tích khối hộp bằng A. 8
a
3
B.
2
3
a
3
C.
8
3
a
3...
Đọc tiếp
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 2a, có đáy là hình vuông và cạnh bên tạo với mặt phẳng đáy khối hộp một góc bằng 60 o Thể tích khối hộp bằng
A. 8 a 3
B. 2 3 a 3
C. 8 3 a 3
D. 4 3 a 3
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a
3
, BD3a. Hình chiếu vuông góc của B trên mặt phẳng (ABCD) trùng với trung điểm A’C’. Gọi
α
là góc giữa 2 mặt phẳng (ABCD) và (CDDC). Thể tích của khối hộp ABCD.ABCD bằng
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , BD=3a. Hình chiếu vuông góc của B trên mặt phẳng (A'B'C'D') trùng với trung điểm A’C’. Gọi α là góc giữa 2 mặt phẳng (ABCD) và (CDD'C'). Thể tích của khối hộp ABCD.A'B'C'D' bằng
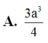
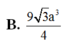
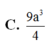
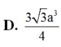
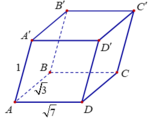
Cho khối hộp ABCD. ABCD có đáy là hình chữ nhật với AB
3
; AD
7
. Hai mặt bên (ABBA) và (ADDA) cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là: A.
7
B.
3
3
C. 5 D.
7
7
Đọc tiếp
Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:
A. 7
B. 3 3
C. 5
D. 7 7