Chọn B.
Ta có (IB'D') và ABCD có I là một điểm chung.
B ' D ' ⊂ ( I B D ) B D ⊂ ( A B C D ) B ' D ' / / B D ⇒ ( I B D ) ∩ ( A B C D ) = I J / / ( J ∈ A D )
Thiết diện là hình thang IJB'D'
Chọn B.
Ta có (IB'D') và ABCD có I là một điểm chung.
B ' D ' ⊂ ( I B D ) B D ⊂ ( A B C D ) B ' D ' / / B D ⇒ ( I B D ) ∩ ( A B C D ) = I J / / ( J ∈ A D )
Thiết diện là hình thang IJB'D'
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A B = B C = a ; A ' A = a 3 . Gọi I là giao điểm của AD' và A’D ; H là hình chiếu của I trên mặt phẳng A ' B ' C ' D ' , K là hình chiếu của B lên mặt phẳng C A ' B ' . Tính thể tích khối tứ diện IHBK ?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 16
D. a 3 3 8
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình chữ nhật , AB = a, AD = 2, hình chiếu vuông góc của điểm A trên mặt phẳng ( A ' B ' C ' D ' ) là trung điểm H của A’D’. Biết rằng AA’ hợp với đáy một góc 60 0 . Gọi α là số đo của góc giữa hai đường thẳng A C , B ' D . Khi đó cos α bằng
![]()
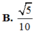
![]()
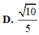
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB//CD). Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
![]()
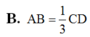
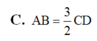
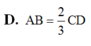
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , B C = a Biết bán kính của mặt cầu ngoại tiếp của hình hộp chữ nhật là 3 a 2 Thể tCho hình hộp chữ nhậích của hình hộp chữ nhật là
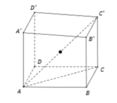
A. a 3 3 2
B. 4 a 3
C. 2 a 3
D. 2 3 a 3
I. Trắc nghiệm ( 6 điểm)
Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c.
A. π a 2 + b 2 + c 2
B. 2 π a 2 + b 2 + c 2
C. 4 π a 2 + b 2 + c 2
D. π 2 a 2 + b 2 + c 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = 2a, AD = 3a. Gọi V là phần thể tích thuộc hình hộp nằm ở khoảng giữa hai mặt phẳng (A'BD) và (B'CD'). Tính V.
A. V = 4 a 3
B. V = 3 a 3
C. V = 2 a 3
D. V = a 3
Cho hai tấm tôn hình chữ nhật đều có kích thước 1,5mx8m. Tấm tôn thứ nhất được chế tạo thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1,5m, còn tấm tôn thứ hai được chế tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1,5m. Gọi
V
1
,
V
2
, theo thứ tự là thể tích của khối hộp chữ nhật và thể tích của khối trụ. Tính tỉ số
V
1
V
2
.

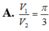
![]()
![]()
![]()