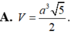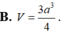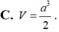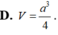Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AA2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
a
3
2
Tính thể tích V của hình hộp chữ nhật ABCD.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
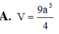
![]()
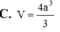
![]()
Cho khối hộp ABCD.ABCD có đáy là hình chữ nhật, AB
3
AD
7
Hai mặt bên (ABBA) (ADDA) tạo với đáy các góc lần lượt là
45
o
và
60
o
. Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1. A. V 3 B. V
7
3...
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB = 3 AD= 7 Hai mặt bên (ABB'A) (ADD'A') tạo với đáy các góc lần lượt là 45 o và 60 o . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
A. V = 3
B. V = 7 3
C. V = 3
D. V = 7
Cho khối hộp chữ nhật ABCD.ABCD. Gọi M là trung điểm của BB. Mặt phẳng (MDC) chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A. Gọi
V
1
,
V
2
lần lượt là thể tích hai khối đa diện chứa C và A. Tính
V
1
V
2
.
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D'. Gọi M là trung điểm của BB'. Mặt phẳng (MDC') chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A'. Gọi V 1 , V 2 lần lượt là thể tích hai khối đa diện chứa C và A'. Tính V 1 V 2 .
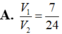
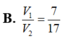
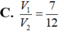
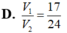
Cho hình hộp chữ nhật ABCD.ABCD có Tính theo thể tích khối hợp đã cho.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có ![]() Tính theo thể tích khối hợp đã cho.
Tính theo thể tích khối hợp đã cho.
![]()
![]()
![]()
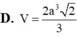
Cho hình hộp chữ nhật ABCD.A'B'C'D; có AB = a, BC = b, CC' = c.
a) Tính khoảng cách từ B đến mặt phẳng (ACC'A').
b) Tính khoảng cách giữa hai đường thẳng BB' và AC'.
Khối hộp chữ nhật có 3 cạnh xuất phát từ một đỉnh lần lượt có độ dài a, b, c. Thể tích khối hộp chữ nhật là ? A.
1
3
a
b
c
B. abc. C.
1
6
a
b
c
D.
4
3
a
b
c
Đọc tiếp
Khối hộp chữ nhật có 3 cạnh xuất phát từ một đỉnh lần lượt có độ dài a, b, c. Thể tích khối hộp chữ nhật là ?
A. 1 3 a b c
B. abc.
C. 1 6 a b c
D. 4 3 a b c
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có AB = a, BC= b, CC'= c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b và c.
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi, cạnh
a
3
. Hình chiếu vuông góc với B trên mặt phẳng (ABCD) là trung điểm AC, mặt phẳng (CDDC) tạo với đáy góc
60
0
.Tính theo a thể tích khối hộp ABCD.ABCD
A
.
9
a
3
8
B
.
a...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a 3 . Hình chiếu vuông góc với B' trên mặt phẳng (ABCD) là trung điểm AC, mặt phẳng (CDD'C') tạo với đáy góc 60 0 .Tính theo a thể tích khối hộp ABCD.A'B'C'D'
A . 9 a 3 8
B . a 3 8
C . 27 a 3 8
D . 2 a 3 3 9
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB a, BC 2a, AA’ a. Lấy điểm I trên cạnh AD sao cho AI 3 ID. Tính thể tích của khối chop B’. IAC.
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB = a, BC = 2a, AA’ = a. Lấy điểm I trên cạnh AD sao cho AI = 3 ID. Tính thể tích của khối chop B’. IAC.