Ta có: V ACB ' D ' V ABCD . A ' B ' C ' D ' = 1 3
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình hộp ABCD.A’B’C’D’ có diện tích các mặt
(
A
B
C
D
)
,
(
A
B
B
A
)
,
(
A
D
D
A
)
lần lượt bằng 20cm2, 28cm2, 35cm2. Tính thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có diện tích các mặt ( A B C D ) , ( A B B ' A ' ) , ( A D D ' A ' ) lần lượt bằng 20cm2, 28cm2, 35cm2. Tính thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’
![]()
![]()
![]()
![]()
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,
BCD
^
120° và AA 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’. A. V 12
a
3
B. V 3
a
3
C. V 9
a
3
D. V 6
a
3
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD ^ = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’. A.
V
2
6
a
3
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = 2 6 a 3
B. V = 2 6 3 a 3
C. V = 3 2 a 3
D. V = 6 a 3
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC a
3
, AD 2a, AB a
5
. Tính thể tích V của hình hộp. A. V
2
a
3
15
B. V
a
3
15
3
C. V
a
3
6
D. V
3
a...
Đọc tiếp
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC = a 3 , AD' = 2a, AB' = a 5 . Tính thể tích V của hình hộp.
A. V = 2 a 3 15
B. V = a 3 15 3
C. V = a 3 6
D. V = 3 a 3
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) với góc 300. Tính thể tích V của khối hộp ABCDA’B’C’D’.
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) với góc 300. Tính thể tích V của khối hộp ABCDA’B’C’D’.
![]()
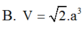
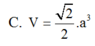
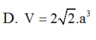
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp. A. A’(-3;2;1) B. A’(-3;-3;3) C. A’(-3;-3;-3) D. A’(-3;3;3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp.
A. A’(-3;2;1)
B. A’(-3;-3;3)
C. A’(-3;-3;-3)
D. A’(-3;3;3)
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Tọa độ của điểm A’ là
Đọc tiếp
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Tọa độ của điểm A’ là
![]()
![]()
![]()
![]()
Hình hộp ABCD.A’B’C’D’ có A(0;0;1),B(-1;1;0),D(-2;-1;0),A'(1;1;0) Tọa độ đỉnh C’ là
A. (1;-1;-2)
B. (2;1;-2)
C. (0;1;-2)
D. (-2;1;-2)
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ với A(-2;1;3), C(2;3;5), B’(2;4;-1), D’(0;2;1). Tìm tọa độ điểm B
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’ với A(-2;1;3), C(2;3;5), B’(2;4;-1), D’(0;2;1). Tìm tọa độ điểm B
![]()
![]()
![]()
![]()



