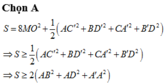Các câu hỏi tương tự
Cho hình chóp S.ABC có AB BC CA a, SA SB SC
a
3
, M là điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng A.
d
2
a
3
B.
a
6
2
C.
a
6
D.
a...
Đọc tiếp
Cho hình chóp S.ABC có AB = BC = CA = a, SA = SB = SC = a 3 , M là điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng
A. d = 2 a 3
B. a 6 2
C. a 6
D. a 3 2
Cho hình chóp S.ABC có
A
B
B
C
C
A
a
,
S
A
S
B
S
C
a
3
, Mlà điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng: A.
d
2
a...
Đọc tiếp
Cho hình chóp S.ABC có A B = B C = C A = a , S A = S B = S C = a 3 , Mlà điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng:
A. d = 2 a 3 .
B. a 6 2 .
C. a 6 .
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
-
2
2
+
z
+
3
2
25
và điểm A(2;2;1). Xét các đi...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y - 2 2 + z + 3 2 = 25 và điểm A(2;2;1). Xét các điểm B, C, D thay đổi thuộc (S) sao cho AB, AC, AD đôi một vuông góc nhau. Khoảng cách từ tâm của (S) đến mặt phẳng (BCD) có giá trị lớn nhất bằng
A. 10 3
B. 1
C. 5 6
D. 5 3
Trong không gian Oxyz, cho
A
(
0
;
0
;
2
)
,
B
(
1
;
1
;
0
)
và mặt cầu
(
S
)
:
x
2
+
y
2
+
(
z
-
1
)
2
1
4...
Đọc tiếp
Trong không gian Oxyz, cho A ( 0 ; 0 ; 2 ) , B ( 1 ; 1 ; 0 ) và mặt cầu ( S ) : x 2 + y 2 + ( z - 1 ) 2 = 1 4 . Xét điểm M thay đổi thuộc (S). Giá trị nhỏ nhất của biểu thức MA 2 + 2 MB 2 bằng:
A . 1 2
B . 3 4
C . 21 4
D . 19 4
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng A.5,5 B. 4,5 C. 6,5 D. 7,5
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 = 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 = 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng
A.5,5
B. 4,5
C. 6,5
D. 7,5
Trong không gian Oxyz, cho mặt phẳng
P
:
2
x
-
y
+
2
z
-
14
0
và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
+
2
z
-
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng
P : 2 x - y + 2 z - 14 = 0 và mặt cầu
S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Gọi tọa độ điểm M (a; b; c) thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất. Tính giá trị biểu thức K = a + b + c.
A. K = -2.
B. K = -5.
C. K = 2.
D. K = 1.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A
B
a
,
A
D
2
a
,
A
A
’
3
a
. Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp(MNP). A.
15
22
a
B.
9
11
a
C....
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = a , A D = 2 a , A A ’ = 3 a . Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp(MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a
Trong không gian Oxyz, cho hai đường thẳng
∆
:
x
1
y
1
z
-
1
1
và
∆
:
x
-
1
1
y
2
z
1...
Đọc tiếp
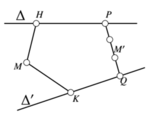
Trong không gian Oxyz, cho hai đường thẳng ∆ : x 1 = y 1 = z - 1 1 và ∆ ' : x - 1 1 = y 2 = z 1 . Xét điểm M thay đổi. Gọi a, b lần lượt là khoảng cách từ M đến D và D’. Biểu thức a 2 + 2 b 2 đạt giá trị nhỏ nhất khi và chỉ khi M ≡ M 0 x 0 ; y 0 ; z 0 . Khi đó x 0 + y 0 bằng
A. 2 3
B. 0
C. 4 3
D. 2
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
A
a
.
Gọi M là điểm trên đoạn AD với
A
D
M
D...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A A ' = a . Gọi M là điểm trên đoạn AD với A D M D = 3 . Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B 'C và y là độ dài khoảng cách từ M đến mặt phẳng A B ' C . Tính giá trị xy
A. 5 a 5 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2