Xét ΔABD vuông tại A có:
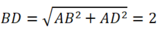
Do ABCD là hình chữ nhật tâm I nên:
AI = IC = ID = 1/2 BD = 1
ΔICD có ID = IC = DC = 1
⇒ΔICD đều ⇒ ∠(DIC) = 60o
Ta có: ∠(DIC) + ∠(AID ) = 180o⇒ ∠(AID ) = 180o- 60o= 120o
Xét ΔABD vuông tại A có:
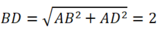
Do ABCD là hình chữ nhật tâm I nên:
AI = IC = ID = 1/2 BD = 1
ΔICD có ID = IC = DC = 1
⇒ΔICD đều ⇒ ∠(DIC) = 60o
Ta có: ∠(DIC) + ∠(AID ) = 180o⇒ ∠(AID ) = 180o- 60o= 120o
Cho hình thoi ABCD tâm I. Biết hai cạnh AB và AD lần lượt có phương trình là 2x - y - 1 = 0 và x - 2y - 5 = 0 , tâm I thuộc Parabol y ^ 2 = x . Tính toạ độ các đỉnh của hình thoi.
Cho hình vuông ABCD có tâm O và trục (i) đi qua O . Xác định số đo góc giữa tia OA với trục (i) , biết trục (i) đi qua trung điểm I của cạnh AB
A. 450 + k.3600
B. 900 + k.3600
C. 600 + k.3600
D. 1200 + k.3600
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0; 3); D(2; 1) và I(-1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC
A. (1 ; 2)
B. (-2; -3)
C. (-3 ; -2)
D. (- 4 ; -1)
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0 ; 3) ; D(2 ; 1) và I( -1 ; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC.
A. (1; 2)
B. (-2; -3)
C. (-3; -2)
D. (-4; -1)
Cho hình chữ nhật ABCD biết AD = 1 . Giả sử E là trung điểm AB và thỏa mãn sin B D E ^ = 1 3 .Tính độ dài cạnh AB.
A. 1
B. 2
C . 2
D. 3
Cho hình thoi abcd Tâm o cạnh a góc BAD Bằng 60 °. Gọi I J lần lượt là trung điểm AB , CD Và K Là trung điểm của I J.
a. CMR: Ka + Kb + Kc + Kd = 0
b. Tính độ dài Vecto AB + AD
cho hình chữ nhật ABCD có AD=1/2 AB=a, I là trọng tâm của tam giác ABD
CM: vecto IA + vecto IB + vecto IC = vecto DC
Cho hình chữ nhật ABCD có cạnh AD=2AB=10cm. Tính độ dài vecto AB+ vecto BD