Các câu hỏi tương tự
Cho hình chữ nhật ABCD có tỉ lệ hai cạnh
A
B
:
A
D
2
:
3
. Khi quay hình chữ nhật xung quanh cạnh AB ta thu được hình trụ có thể tích
V
1
, khi quay hình chữ nhật quanh cạnh AD ta thu được hình trụ có thể tích
V
2
. Tính tỉ số thể tích
V
1
V...
Đọc tiếp
Cho hình chữ nhật ABCD có tỉ lệ hai cạnh A B : A D = 2 : 3 . Khi quay hình chữ nhật xung quanh cạnh AB ta thu được hình trụ có thể tích V 1 , khi quay hình chữ nhật quanh cạnh AD ta thu được hình trụ có thể tích V 2 . Tính tỉ số thể tích V 1 V 2 .
A. 3 2 .
B. 2 3 .
C. 2 5 .
D. 3 5 .
Trong không gian cho ABCD là hình chữ nhật, AB2, AD1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
(
A
B
,
d
)
d
(
C
D
,
d
)
. Tính a biết rằng thể t...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Trong không gian cho hình chữ nhật ABCD có
AD
a
,
AC
3
a
.
. Tính theo a độ dài đường sinh l của hình trụ, nhận được khi quay hình chữ nhật ABCD xung quanh trục AB. A.
10
a
B.
2
2
a
C.
3
a
D.
2
3
a
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có AD = a , AC = 3 a . . Tính theo a độ dài đường sinh l của hình trụ, nhận được khi quay hình chữ nhật ABCD xung quanh trục AB.
A. 10 a
B. 2 2 a
C. 3 a
D. 2 3 a
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB. A.
S
x
q
2
π
a
2
.
B....
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB.
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
Cho hình chữ nhật ABCD có AB a, AD
a
3
. Tính diện tích xung quanh của hình tròn xoay sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB A.
12
π
a
2
B.
12
π
a
2
3
C.
6
a
2
3
D....
Đọc tiếp
Cho hình chữ nhật ABCD có AB = a, AD = a 3 . Tính diện tích xung quanh của hình tròn xoay sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB
A. 12 π a 2
B. 12 π a 2 3
C. 6 a 2 3
D. 2 π a 2 3
Trong không gian, cho hình chữ nhật ABCD có AB 2, AD 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d. A.
V
17
π
B.
V
5
π
C.
V
15
π
D.
V
30
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. V = 30 π
Diện tích và chu vi của một hình chữ nhật ABCD (AB AD) theo thứ tự là
2
a
2
và 6a. Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này. A.
4
π
a
3
;
4
π
a
2
B.
2
π
a
3...
Đọc tiếp
Diện tích và chu vi của một hình chữ nhật ABCD (AB > AD) theo thứ tự là 2 a 2 và 6a. Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này.
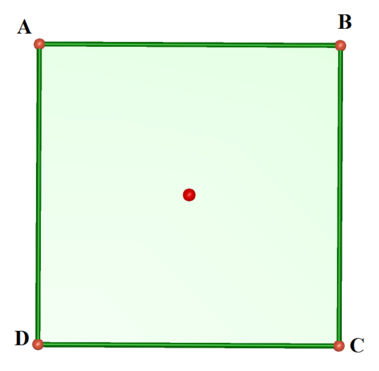
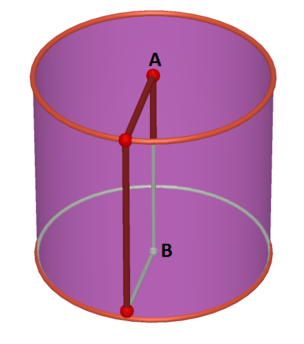
A. 4 π a 3 ; 4 π a 2
B. 2 π a 3 ; 4 π a 2
C. 2 π a 3 ; 2 π a 2
D. 4 π a 3 ; 2 π a 2
Diện tích và chu vi của một hình chữ nhật ABCD (AB AD) theo thứ tự là
2
a
2
và
6
a
. Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này. A.
2
πa
3
;
4
πa
2
B.
4
πa
3
;
4
πa...
Đọc tiếp
Diện tích và chu vi của một hình chữ nhật ABCD (AB > AD) theo thứ tự là 2 a 2 và 6 a . Cho hình chữ nhật quay quanh cạnh AB một vòng, ta được một hình trụ. Tính thể tích và diện tích xung quanh của hình trụ này.
A. 2 πa 3 ; 4 πa 2
B. 4 πa 3 ; 4 πa 2
C. 2 πa 3 ; 2 πa 2
D. 4 πa 3 ; 2 πa 2
Trong không gian cho hình chữ nhật ABCD có AB2, AD1. Gọi
V
1
,
V
2
lần lượt là thể tích khối trụ nhận được khi quay hình chữ nhật ABCD xung quanh trục AB và AD. Hệ thức nào sau đây là đúng? A.
V
2
4
V
1
B.
V
2
2...
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có AB=2, AD=1. Gọi V 1 , V 2 lần lượt là thể tích khối trụ nhận được khi quay hình chữ nhật ABCD xung quanh trục AB và AD. Hệ thức nào sau đây là đúng?
A. V 2 = 4 V 1
B. V 2 = 2 V 1
C. V 2 = V 1
D. V 2 = V 1 2