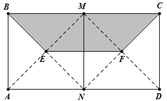
Các câu hỏi tương tự
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết
A
B
4
,
A
D
7
. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN. A.
104
3
π
B.
116
3
π
C.
44
3
π
D....
Đọc tiếp
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết A B = 4 , A D = 7 . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
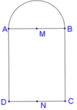
A. 104 3 π
B. 116 3 π
C. 44 3 π
D. 1000 3 π
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M,N lần lượt là trung điểm của AB,CD. Biết
AB
4
,
AD
7
. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN. A.
44
3
π
B.
24
3
π
C.
100
3
π
D. ...
Đọc tiếp
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M,N lần lượt là trung điểm của AB,CD. Biết AB = 4 , AD = 7 . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
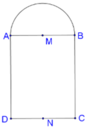
A. 44 3 π
B. 24 3 π
C. 100 3 π
D. 116 3 π
Cho hình chữ nhật ABCD có cạnh AB=4,AD=6. Gọi M,N lần lượt là trung điểm của AD,BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN.
A. 36π
B. 12π
C. 24π
D. 18π
Cho hình chữ nhật ABCD có cạnh
AB
4
,
AD
6
. Gọi M, N lần lượt là trung điểm của AD, BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN. A.
18
π
B.
12
π
C.
36
π
D.
24
π
Đọc tiếp
Cho hình chữ nhật ABCD có cạnh AB = 4 , AD = 6 . Gọi M, N lần lượt là trung điểm của AD, BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN.
A. 18 π
B. 12 π
C. 36 π
D. 24 π
Cho hình chữ nhất ABCD có cạnh AB 6, AD 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhất ABCD quay quanh QN, khi đó tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng
A
.
4
π
B
.
8
π
C
.
10
π
D
.
24
π
Đọc tiếp
Cho hình chữ nhất ABCD có cạnh AB = 6, AD = 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhất ABCD quay quanh QN, khi đó tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng
A . 4 π
B . 8 π
C . 10 π
D . 24 π
Một hình thang vuông ABCD có đường cao
A
D
π
, đáy nhỏ
A
B
π
, đáy lớn
C
D
2
π
. Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng: A.
4
3
π
4
B.
7
3
π
4
C.
10
3...
Đọc tiếp
Một hình thang vuông ABCD có đường cao A D = π , đáy nhỏ A B = π , đáy lớn C D = 2 π . Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4
Cho hình chữ nhật ABCD cạnh AB 4; AD 2. Gọi M,N lần lượt là trung điểm AB và CD. Cho hình chữ nhật quay quanh MN ta thu được hình trụ tròn xoay. Tính thể tích của hình trụ tròn xoay. A. V 4
π
B. V 8
π
C. V 16
π
D. V 32
π
Đọc tiếp
Cho hình chữ nhật ABCD cạnh AB = 4; AD = 2. Gọi M,N lần lượt là trung điểm AB và CD. Cho hình chữ nhật quay quanh MN ta thu được hình trụ tròn xoay. Tính thể tích của hình trụ tròn xoay.
A. V = 4 π
B. V = 8 π
C. V = 16 π
D. V = 32 π
Hình chữ nhật ABCD có
A
B
4
,
A
D
2
. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng A.
V
4
π
3
B.
V
8
π
C.
V
8
π
3...
Đọc tiếp
Hình chữ nhật ABCD có A B = 4 , A D = 2 . Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
A. V = 4 π 3
B. V = 8 π
C. V = 8 π 3
D. V = 32 π
Hình chữ nhật ABCD có AB4, AD2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng A.
V
4
π
3
.
B.
V
8
π
.
C.
V
8
π
3
....
Đọc tiếp
Hình chữ nhật ABCD có AB=4, AD=2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
A. V = 4 π 3 .
B. V = 8 π .
C. V = 8 π 3 .
D. V = 32 π .