Các câu hỏi tương tự
Một hình thang vuông ABCD có đường cao
A
D
π
, đáy nhỏ
A
B
π
, đáy lớn
C
D
2
π
. Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng: A.
4
3
π
4
B.
7
3
π
4
C.
10
3...
Đọc tiếp
Một hình thang vuông ABCD có đường cao A D = π , đáy nhỏ A B = π , đáy lớn C D = 2 π . Cho hình thang đó quay quanh CD, ta được vật tròn xoay có thể tích bằng:
A. 4 3 π 4
B. 7 3 π 4
C. 10 3 π 4
D. 13 3 π 4
Cho hình trụ (T)có bán kính bằng 4 cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB CD 5 cm. Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng
60
°
. Thể tích của khối trụ là: A.
60
π
3
cm
3
B.
24
π
13
cm
3...
Đọc tiếp
Cho hình trụ (T)có bán kính bằng 4 cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB = CD = 5 cm. Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng 60 ° . Thể tích của khối trụ là:
A. 60 π 3 cm 3
B. 24 π 13 cm 3
C. 16 π 13 cm 3
D. 48 π 13 cm 3
Cho hình chữ nhật ABCD có tỉ lệ hai cạnh
A
B
:
A
D
2
:
3
. Khi quay hình chữ nhật xung quanh cạnh AB ta thu được hình trụ có thể tích
V
1
, khi quay hình chữ nhật quanh cạnh AD ta thu được hình trụ có thể tích
V
2
. Tính tỉ số thể tích
V
1
V...
Đọc tiếp
Cho hình chữ nhật ABCD có tỉ lệ hai cạnh A B : A D = 2 : 3 . Khi quay hình chữ nhật xung quanh cạnh AB ta thu được hình trụ có thể tích V 1 , khi quay hình chữ nhật quanh cạnh AD ta thu được hình trụ có thể tích V 2 . Tính tỉ số thể tích V 1 V 2 .
A. 3 2 .
B. 2 3 .
C. 2 5 .
D. 3 5 .
Cho hình chữ nhật ABCD có
AB
2
,
AD
4
. Tính thể tích V của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh trục CD A.
24
π
B.
32
π
3
C.
32
π
D.
16
π
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 2 , AD = 4 . Tính thể tích V của khối trụ tạo thành khi quay hình chữ nhật ABCD quanh trục CD
A. 24 π
B. 32 π 3
C. 32 π
D. 16 π
Trong không gian cho ABCD là hình chữ nhật, AB2, AD1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
(
A
B
,
d
)
d
(
C
D
,
d
)
. Tính a biết rằng thể t...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Trong không gian, cho hình chữ nhật ABCD có AB 2, AD 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d. A.
V
17
π
B.
V
5
π
C.
V
15
π
D.
V
30
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. V = 30 π
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
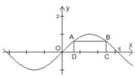
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho một tấm nhôm hình chữ nhật ABCD có AD 60 cm. Ta gập tấm nhôm theo hai cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau, với AN PD (như hình vẽ dưới đây) để được một hình lăng trụ. Tìm độ dài đoạn AN để thể tích khối lăng trụ lớn nhất. A. AN 39 cm B. AN 20 cm C. AN
15
2
cm D. AN 15 cm
Đọc tiếp
Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm. Ta gập tấm nhôm theo hai cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau, với AN = PD (như hình vẽ dưới đây) để được một hình lăng trụ. Tìm độ dài đoạn AN để thể tích khối lăng trụ lớn nhất.
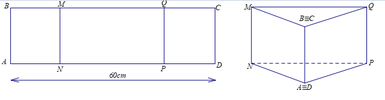
A. AN = 39 cm
B. AN = 20 cm
C. AN = 15 2 cm
D. AN = 15 cm
Cho hình chữ nhật ABCD có chiều dài
A
B
2
A
D
. Quay hình chữ nhật quay quanh cạnh AB sinh ra khối trụ có thể tích
V
1
và quay hình chữ nhật đó quanh cạnh AD sinh ra hìnhtrụ có thể tích
V
2
. Tỉ số
V
1
V
2
là A.
27...
Đọc tiếp
Cho hình chữ nhật ABCD có chiều dài A B = 2 A D . Quay hình chữ nhật quay quanh cạnh AB sinh ra khối trụ có thể tích V 1 và quay hình chữ nhật đó quanh cạnh AD sinh ra hình
trụ có thể tích V 2 . Tỉ số V 1 V 2 là
A. 27 π 2 .
B. 1 2 .
C. π 2 .
D. 27



