Đáp án C


Xét hàm
f t = t − t 3 ; f ' t = 1 − 3 t 2 ; f ' t = 0 ⇔ t = − 1 3 t = 1 3
Ta có bảng biến thiên trên 0 ; 1
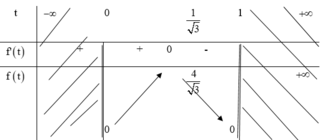
Vậy giá trị nhỏ nhất của V đạt được khi f t lớn nhất tức là min V = 16 3
Đáp án C



Xét hàm
f t = t − t 3 ; f ' t = 1 − 3 t 2 ; f ' t = 0 ⇔ t = − 1 3 t = 1 3
Ta có bảng biến thiên trên 0 ; 1

Vậy giá trị nhỏ nhất của V đạt được khi f t lớn nhất tức là min V = 16 3
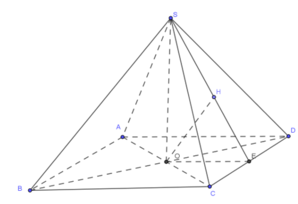
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ A đến S C D bằng 4. Gọi V là thể tích khối chóp S.ABCD, tính giá trị lớn nhất của V
A. 32 3
B. 8 3
C. 16 3
D. 16 3 3
Cho hình chóp tứ giác đều S.ABCD đỉnh S , khoảng cách từ C đến mặt phẳng (SAB) bằng 6 . Gọi V là thể tích khối chóp S.ABCD, tính giá trị nhỏ nhất của V
A. 18 3
B. 64 3
C. 27 3
D. 54 3
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và có thể tích V = a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy.
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho hình chóp đều S.ABCD có khoảng cách từ A đến mặt phẳng (SCD) bằng a. Tính giá trị nhỏ nhất của thể tích khối chóp S.ABCD theo a.
A. a 3 3 6
B. a 3 3 2
C. a 3 3 4
D. a 3 3 3
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ tâm O của đáy đến (SCD) bằng 2a, a là hằng số dương. Đặt AB=x. Giá trị của x để thể tích của khối chóp SABCD đạt giá trị nhỏ nhất là
A. a 3
B. 2 a 6
C. a 2
D. a 6
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm B đến mặt phẳng (SCD) bằng 3 7 a 7 . Tính thể tích V của khối chóp S.ABCD
A. V = 1 3 a 3
B. V = a 3
C. V = 2 3 a 3
D. V = 3 2 a 3
Xét hình chóp từ giác đều S.ABCD có tam giác SAC nội tiếp trong đường tròn có bán kính bằng 9. Gọi d là khoảng cách từ S đến mặt phẳng (ABCD) và T là diện tích tứ giác ABCD. Tính d khi biểu thức P = d . T đạt giá trị lớn nhất.
A. d = 10
B. d = 17
C. d = 15
D. d = 12
Xét hình chóp từ giác đều S.ABCD có tam giác SAC nội tiếp trong đường tròn có bán kính bằng 9. Gọi d là khoảng cách từ S đến mặt phẳng (ABCD) và T là diện tích tứ giác ABCD. Tính d khi biểu thức P = d . T đạt giá trị lớn nhất.
A. d = 10
B. d = 17
C. d = 15
D. d = 12
Hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Thể tích của hình chóp V = 3 a 3 . Hỏi khoảng cách từ S đến mặt phẳng (ABCD) bằng bao nhiêu?
A. 3a
B. 6a
C. 9a
D. a