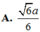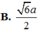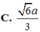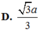Question

: Cho hình chóp S.ABCD có SA⊥(ABCD) và SA=a; đáy ABCD là hình thang vuông có đáy bé là BC, biết AB=BC=a, AD=2a.

1) Chứng minh các mặt bên của hình chóp là các tam giác vuông

2) Tính khoảng cách giữa AB và SD

3) M, H là trung điểm của AD, SM cm AH⊥(SCM)

4) Tính góc giữa SD và (ABCD); SC và (ABCD)

5) Tính góc giữa SC và (SAD)

6) Tính tổng diện tích các mặt của chóp.

Answer 1

1: SA vuông góc (ABCD)

=>SA vuông góc AB

=>ΔSAB vuông tại A

SA vuông góc (ABCD)

=>SA vuông góc AD

=>ΔSAD vuông tại A

4: (SD;(ABCD))=(DS;DA)=góc SDA

tan SDA=SA/AD=1/2

=>góc SDA=27 độ

(SC;(ABCD))=(CS;CA)=góc SCA

AC=căn a^2+a^2=a*căn 2

tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ