Đáp án D
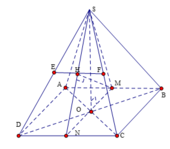
Vì AB//(SCD) => khoảng cách d giữa AB bằng khoảng cách giữa AB và (SCD)
Gọi M, N lần lượt là trung điểm của AB, CD khi đó AB ⊥ (SMN)
Kẻ đường cao MH của ∆ SMN => MH là khoảng cách giữa AB và SC
Ta có:
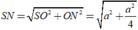
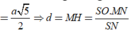
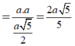
Đáp án D

Vì AB//(SCD) => khoảng cách d giữa AB bằng khoảng cách giữa AB và (SCD)
Gọi M, N lần lượt là trung điểm của AB, CD khi đó AB ⊥ (SMN)
Kẻ đường cao MH của ∆ SMN => MH là khoảng cách giữa AB và SC
Ta có:
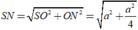
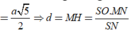
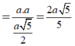
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và SO=a. Khoảng cách giữa SC và AB bằng
A. 2 a 5 5
B. a 5 5
C. 2 a 3 15
D. a 3 15
Bài 5: Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O, cạnh SA vuông góc với mặt đáy. là mặt phẳng đi qua A và vuông góc với SC, cắt SC tại I.
a) Xác định giao điểm K của SO với .
b) Chứng minh: và .
c) Xác định giao tuyến của mặt phẳng và . Tìm thiết diện cắt hình chóp S.ABCD bởi .
giúp mình đc ko mọi người? em cảm ơn rất nhiều
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với 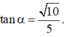 Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
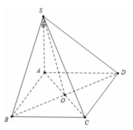
A. 60 o
B. 69 , 3 o
C. 90 o
D. 45 o
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, cạnh a SA vuông góc với mặt phẳng (ABCD) và SA=a căn 2. Tính khoảng cách từ:
a) C đến mặt phẳng (SAB).
b) từ A đến (SCD).
c) Từ O đến (SCD).
d) Khoảng cách giữa hai đường thẳng AB và SC.
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là một hình vuông tâm O cạnh 2a, SO vuông góc (ABCD) và \(SO=a\sqrt{6}\)
a: Chứng minh \(\left(SAC\right)\perp\left(SBD\right)\)
b: Tính \(\widehat{SC;\left(ABCD\right)}\)
c: Tính khoảng cách giữa AB và mp(SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a Tính góc giữa đường thẳng SC và mặt phẳng (SBD)
A. arcsin 1 4 B. arcsin 1 3 C. arcsin 1 3 D. arcsin 2 3
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc B A D ^ = 60 o . Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và S O = 3 a 4 . Khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 3 2
B. 3 a 2
C. 2 a 3
D. 3 a 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng
A. a 3 4
B. a 6 3
C. a 2
D. a 6 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 10. Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC = 10√5. Gọi M,N lần lulư là trung điểm của SA và CD. Tính khoảng cách d giữa BD và MN.
A. d=3√5
B. d=√5
C. d=5
D. d=10