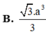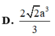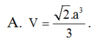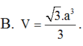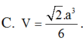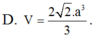Question

Cho hình chóp SABCD có đáy là hình thoi biết AC =3a,BD=5a SB vuông góc với đáy góc giữa SC và đáy 60 độ Tính thể tích khối chóp SABCD theo a

Answer 1

Có: (SC, (ABCD)) = ∠SCB

Gọi: \(O=AC\cap BD\)

Có: \(OC=\dfrac{1}{2}AC=\dfrac{3}{2}a\)

\(OB=\dfrac{1}{2}BD=\dfrac{5}{2}a\)

Xét tam giác OBC vuông tại O (Do: ABCD là hình thoi nên AC ⊥ BD), có:

\(BC=\sqrt{OB^2+OC^2}=\dfrac{a\sqrt{34}}{2}\)

Xét tam giác SBC vuông tại B (Do: SB ⊥ (ABCD) ), có:

\(SB=BC.tan60^o=\dfrac{a\sqrt{102}}{2}\)

\(\Rightarrow V_{SABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{102}}{2}.\dfrac{1}{2}.3a.5a=\dfrac{5a^3\sqrt{102}}{4}\left(đvtt\right)\)