Đáp án B.
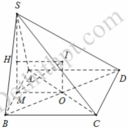
Gọi O là tâm của hính vuông ABCD và H là tâm của đường tròn ngoại tiếp Δ S A B . Từ O kẻ đường thẳng d vuông góc với (ABCD). Từ H kẻ đường thẳng H vuông góc với (SAB).
Ta có d ∩ Δ = I ⇒ I A = I B = I C = IS ⇒ I là tâm đường tròn ngoại tiếp khối chóp S . A B C D ⇒ R = I A = O I 2 + O A 2 .
Mà O I = H M = H B 2 − M B 2 với M là trung điểm của AB.
Xét Δ S A B cân tại S, có A B sin A S B ^ = 2 r
⇒ H B = r = 2 a 2. sin 120 0 = 2 a 3 .
Khi đó O I = 2 a 3 2 − a 2 = a 3 ⇒ R = a 3 2 + a 2 2 = a 21 3 .



