Question

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a*. Cạnh bên SA vuông góc với đáy và S B D   =   60 0 . Tính khoảng cách giữa hai đường thẳng AB và SO.

A.  a 5 2

B. a 2 2

C. a 2 5

D. a 5 5

Answer 1

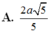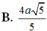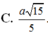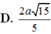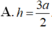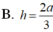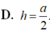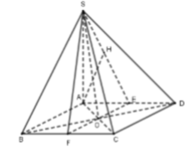
Phương pháp:

- Dựng mặt phẳng chứa SO và song song với AB .

- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.

- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận.

Cách giải:

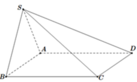
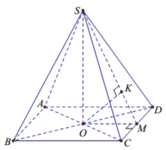
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF => AB / / (SEF) 

Mà 

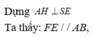
ABCD là hình vuông cạnh a nên BD =  a 2

Dễ dàng chứng minh được

Tam giác SBD cân có  S B D   =   60 0  

Tam giác SAD vuông tại A có

Tam giác SAE vuông tại A có 

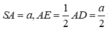
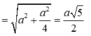
Do đó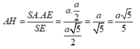 

 

Chọn D.