● SA ⊥ (ABCD) ⇒ SA ⊥ AB, SA ⊥ AD.
⇒ Các tam giác SAB, SAD vuông tại A.
● BC ⊥ SA, BC ⊥ AB.
⇒ BC ⊥ SB ⇒ ΔSBC vuông tại B.
● CD ⊥ SA, CD ⊥ AD.
⇒ CD ⊥ SD ⇒ ΔSCD vuông tại D.
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 3 6 . Độ dài cạnh bên SA bằng bao nhiêu?
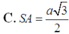
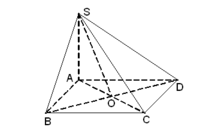
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Tam giác SBD là tam giác vuông.
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD);
b) Tam giác SBD là tam giác vuông tại S.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a Cạnh bên SA vuông góc với mặt phẳng đáy. Trong các tam giác sau, tam giác nào không phải là tam giác vuông?
A. △ S A B
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và SA= a 2 Tính thể tích V của khối chóp S.ABCD
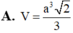
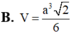
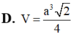
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC = a 5 . Tính thể tích khối chóp.
A . V = a 3 3 3
B . V = a 3 3 6
C . V = a 3 3
D . V = a 3 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Chứng minh rằng: (SAC) ⊥ (SBD).
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)
tại H. Chứng minh rằng
a) OA⊥BC,OB⊥AC,OC⊥AB
b) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BC
c) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giác
ABC.
d)
Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minh
rằng các mặt bên của hình chóp là các tam giác vuông.
Bài 8. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D với AD=DC=AB/2 . Gọi I là trung điểm của đoạn AB, SA vuông góc với mặt đáy. Chứng minh rằng
a) Tam giác ABC vuông tại C
b) CI⊥SB,DI⊥SC
c)CB⊥(SAC)
và các mặt bên hình chóp là các tam giác vuông
