Chọn B.
Phương pháp:
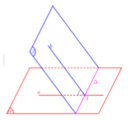

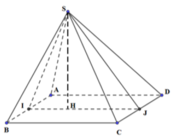
Gọi I, J lần lượt là trung điểm của AB, CD.

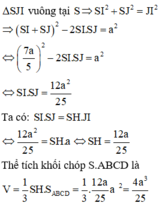
Chọn B.
Phương pháp:



Gọi I, J lần lượt là trung điểm của AB, CD.

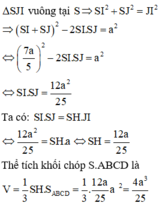
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, biết SA=SB, SC=SD, S A B ⊥ S C D . Tổng diện tích hai tam giác SAB, SCD bằng 7 a 2 10 . Thể tích khối chóp S.ABCD là :
A. 4 a 3 25
B. 4 a 3 15
C. a 3 5
D. a 3 15
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 ° . Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 15 6
B. V = a 3 3 6
C. V = a 3 3 3
D. V = a 3 15 3
Cho hình chóp S.ABCD có đáyABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD).Biết rằng cosin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính a theo thể tích V của khối chóp S.ABCD
A. V = 19 a 3 6
B. V = 15 a 3 6
C. V = 19 a 3 2
D. V = 15 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết góc tạo bởi mặt phẳng (SCD) và đáy bằng 30 0 và khoảng cách từ A tới mặt phẳng (SCD) bằng a. Khi đó thể tích V của khối chóp S.ABCD bằng bao nhiêu?
A. 8 3 a 3 3 .
B. 2 3 a 3 3 .
C. 4 3 a 3 9 .
D. 8 3 a 3 9 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A. πa 3 3
B. 2 πa 3 3
C. πa 3 6
D. 11 11 πa 3 162
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA = SB; SC = SD và hai mặt phẳng (SAB), (SCD) vuông góc với nhau. Tổng diện tích của hai tam giác SAB, SCD, bằng 17 a 2 26 . Tính thể tích V của khối chóp S.ABCD.
A. V = 2 a 3 13 .
B. V = 5 a 3 26 .
C. V = 20 a 3 169 .
D. V = 22 a 3 169 .
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, SA=2a. Thể tích khối chóp S.ABCD theo a là:
A. a 3 15 6
B. a 3 15 12
C. 2 a 3 3
D. 2 a 3
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SA = 2a . Tính theo a thể tích khối chóp S.ABCD.
A. V = a 3 15 12
B. V = a 3 15 6
C. V = 2 a 3 3
D. V = 2 a 3
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,SA=SB,SC=SD. Biết (SAB) ⊥ (SCD) và tổng diện tích của hai tam giác SAB,SCD bằng 7 a 2 10 . Tính thể tích V của khối chóp S.ABCD.
A. V = 4 75 a 3
B. V = 4 15 a 3
C. V = 4 25 a 3
D. V = 12 25 a 3