Đáp án A
Phương pháp: Sử dụng công thức ![]()
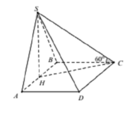
Cách giải: ![]()
Ta có ![]()
Xét tam giác vuông SHC có ![]()
Ta có:
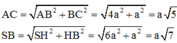
Ta có:
![]()
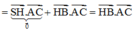
![]()
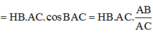
![]()
Lại có ![]()

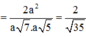
Đáp án A
Phương pháp: Sử dụng công thức ![]()

Cách giải: ![]()
Ta có ![]()
Xét tam giác vuông SHC có ![]()
Ta có:
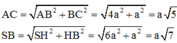
Ta có:
![]()
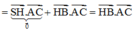
![]()
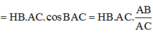
![]()
Lại có ![]()

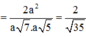
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = 2 a , B C = a . Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 60 ° Tính góc giữa hai đường thẳng SB và AC.
A. 60 °
B. 19 ° 45 ' 31 , 78 ' '
C. 70 ° 14 ' 28 , 22 ' '
D. 57 ° 41 ' 18 , 48 ' '
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với A B = a 2 ; B C = a và S A = S B = S C = S D = 2 a . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
A. 7 4
B. 1 3
D. 8 5
D. 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Hình chiếu của S trên mặt đáy là trung điểm H của OA ; góc giữa hai mặt phẳng (SCD) và ( ABCD) bằng 45 0 . Tính khoảng cách giữa hai đường thẳng AB và SC
A. a 2
B. 3 a 2 2
C. 3 a 2 4
D. a 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
2 a 5 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a, SA vuông góc với mặt phẳng đáy và M là trung điểm của BC, góc giữa đường thẳng SC và mặt phẳng đáy bằng 60 0 . Góc giữa SM và mặt phẳng đáy có giá trị gần với giá trị nào nhất sau đây:
A. 70 0
B. 80 0
C. 90 0
D. 60 0
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , A B = a , B C = a 3 . Tam giác SAO cân tại S, mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 60 0 . Tính khoảng cách giữa 2 đường thẳng SB và AC
A. a 3 2
B. 3 a 2
C. a 2
D. 3 a 4
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 5
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
A. 5 5
B. 2 5 5
C. 1 2
D. 1