Đáp án C
Ta có: Xét ∆ A D H vuông tại A có:
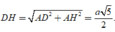
Xét ∆ S D H vuông tại H có:
![]()
S H K D C = 5 S A B C D 8 = 5 a 2 8 (đvdt)
⇒ V S . H K D C = 1 3 . 5 a 2 8 . a 3 = 5 a 3 3 24 (đvtt)
Đáp án C
Ta có: Xét ∆ A D H vuông tại A có:
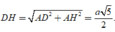
Xét ∆ S D H vuông tại H có:
![]()
S H K D C = 5 S A B C D 8 = 5 a 2 8 (đvdt)
⇒ V S . H K D C = 1 3 . 5 a 2 8 . a 3 = 5 a 3 3 24 (đvtt)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = 13 2 . Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Thể tích khối chóp S.ABCD là:
A. a 3 2 3
B. a 3 12
C. a 3 3
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AD. Tính thể tích khối chóp S.ABCD biết SB = 3a/2.
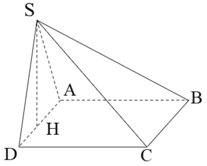
A. a 3 3
B. a 3
C. a 3 2
D. 3 a 3 2
Hình chóp S.ABCD đáy là hình vuông cạnh a, SD = a 13 /2. Hình chiếu của S lên (ABCD) là trung điểm H của AB. Thể tích khối chóp là
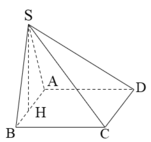
A. a 3 2 3
B. 2 a 3 3
C. a 3 12
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= 3 a 2 , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
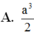
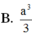
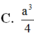
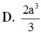
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=2a, AD=a. Hình chiếu của S lên đáy là trung điểm H của cạnh AB, góc tạo bởi SC và đáy bằng 45 0 . Tính thể tích khối chóp S.ABCD
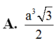

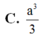
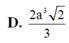
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD, M là trung điểm của CD, cạnh bên SB hợp với đáy một góc 60 ° . Thể tích của khối chóp S.ABCD là
A. a 3 15 6
B. a 3 15 12
C. a 3 15 3
D. a 3 15 4
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD=3CB=3a, AB=a, SA=a 3 . Điểm I thỏa mãn A D → = 3 A I → , M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD)
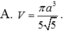
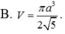
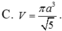
![]()
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:
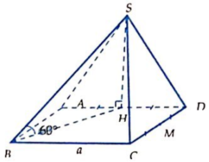
A. a 3 15 3
B. a 3 15 4
C. a 3 15 6
D. a 3 15 12