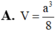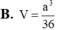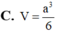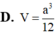Question

Cho hình chóp SABCD có ABCD là hình bình hành. Cho M là điểm thuộc cạnh SA sao cho SM= 1/3 SA. N thuộc cạnh SC sao cho SN = 2NC. E là trung điểm SD. Tìm giao điểm của

 

a/ MN và (ABCD)

 

b/ MN và (SBD)

Answer 1

a.

\(\left\{{}\begin{matrix}M\in SA\in\left(SAC\right)\\N\in SC\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow MN\in\left(SAC\right)\)

Trong mp (SAC), nối MN cắt AC kéo dài tại F

\(\left\{{}\begin{matrix}F\in MN\\F\in AC\in\left(SAC\right)\end{matrix}\right.\)

\(\Rightarrow F=MN\cap\left(SAC\right)\)

b.

Gọi O là giao điểm AC và BD

\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)

\(\Rightarrow\left\{{}\begin{matrix}SO\in\left(SAC\right)\\SO\in\left(SBD\right)\end{matrix}\right.\)

Trong mp (SAC), nối SO cắt MN tại G

\(\left\{{}\begin{matrix}G\in MN\\G\in SO\in\left(SBD\right)\end{matrix}\right.\)

\(\Rightarrow G=MN\cap\left(SBD\right)\)

Answer 2