Ta có:
DC // AB vì tứ giác `ABCD` là hình vuông
`=> (SA,DC) = (SA,AB)`
Do `SA = SB = a sqrt{2}`
`AB = 2a`
`=> SA^2 + SB^2 = AB^2` và tam giác SAB cân tại S
=> Tam giác SAB vuông cân tại S
`=> hat{SAB} = 45^o`
`=> (SA,DC) = (SA,AB) = 45^o`
Vậy ...
Cho hình chóp SABCD. Đáy là hình vuông cạnh 2a; SA= a căn 5. SA vuông góc với đáy a) Tính góc giữa SC và (SAD); góc giữa SB và (SAC) b)Tính góc giữa (SBC) và (ABCD) c)Tính khoảng cách từ SD đến BC
Cho hình chóp SABCD. Đáy là hình vuông cạnh 2a; SA= a căn 5. SA vuông góc với đáy a) Tính góc giữa SC và (SAD); góc giữa SB và (SAC) b)Tính góc giữa (SBC) và (ABCD) c)Tính khoảng cách từ SD đến BC
Cho hình chóp SABCD có SA vuông góc với (ABCD) ; đáy ABCD là hình thang vuông tai A và D, AD=DC =a , AB= 2a, SA = a✓3
@) CM CD vuong với (SAD)
B) CM (SAC) vuông voi (SBC)
C) tính góc giua SB và (ABCD) goc giữa SC va (SAB)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
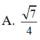
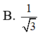
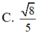
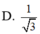
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp SABCD có đáy là hình thang vuông tại A và D. AB=2a, AD=DC=a. Kẻ AH vuông góc với SC (H thuộc SC). E là trung điểm của AB. Sa vuông góc với (ABCD) và SA=a căn 3. Tính góc giữa a)(SBC) và (ABCD) b)(SAD) và (SAC) c)(SBC) và (SCD)
Cho hình chóp S.ABCD có SA ⊥ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. a 3 3
B. a 3 4
C. a 2 3
D. a 2 4
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Cho hình chóp SABCD đáy là hình thoi tâm O cạnh a. (SAD) và (SAC) cùng vuông góc với đáy. Góc BAD=120°, SA=a căn 2. Tính khoảng cách từ a)SB đến CD b)BD đến SC c)SC đến AB
