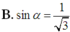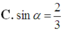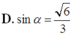Ta thấy hình chiếu vuông góc của  lên
lên  là
là  nên
nên  .
.
Mà  nên
nên  .
.
Vậy góc giữa đường thẳng  và mặt phẳng
và mặt phẳng  bằng
bằng  .
.
Ta thấy hình chiếu vuông góc của  lên
lên  là
là  nên
nên  .
.
Mà  nên
nên  .
.
Vậy góc giữa đường thẳng  và mặt phẳng
và mặt phẳng  bằng
bằng  .
.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA=\(a\sqrt{2}\), AC=2a và SA⊥(ABCD). Tính góc giữa 2 mp (SBC) và (ABC)
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB = 2a, góc giữa (SBC) và mặt đáy bằng 60 0 . Thể tích khối chóp S.ABC là:
A . 125 2 a 3 6
B . 3 6 a 3 4
C . 16 2 a 3 3
D . 2 6 a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = a 2 , SA vuông góc với mp đáy. Góc tạo bởi (SBC) và mặt đáy bằng bao nhiêu
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, A B = 2 a , S A vuông góc với mặt đáy và góc giữa SB với mặt đáy bằng 60 ° . Côsin góc giữa hai mặt phẳng (SBC) và (ABC) bằng
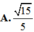
![]()
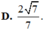
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° khi và chỉ khi SA bằng
![]()
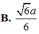
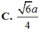
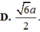
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy ABC, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60°. Tính thể tích V của khối chóp S.ABC.
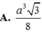
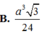
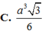
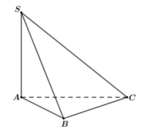
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB =a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 o (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng
A. a
B. a 2 2
C. a 3 2
D. a 3 3
cho hình chóp S.ABC có đáy là tam giác ABC vuông tai B; SA = AB = BC = a và SA vuông góc (ABC). Chứng minh rằng:
a) BC vuông góc (SAB)
b) BC vuông góc SA
c) tìm góc giữa AC và (SBC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
![]()