Đáp án C
Ta có: S A ⊥ B C , A B ⊥ B C
⇒ B C ⊥ ( S A B )
Do đó
![]()
Đáp án C
Ta có: S A ⊥ B C , A B ⊥ B C
⇒ B C ⊥ ( S A B )
Do đó
![]()
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn B I → = 3 I H → . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:
A. V = a3/9
B.V = a3/6
C.V = a3/18
D.V = a3/3
Cho hình chóp S. ABC có đáy ABC là tam giác cân tại A, biết AB = a; SA = SB = a và mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Tính SC biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a.
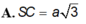
![]()
![]()
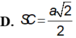
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao S O = a 3 và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a
A. a 3 3 .
B. 2 a 3 .
C. a 3 2 .
D. a
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a , góc ABC = 60 o . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16
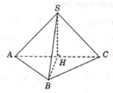
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, đỉnh S cách đều các điểm A,B,C. Biết AC = 2a,BC = a; góc giữa đường thẳng SB và mặt đáy (ABC) bằng 60 o . Tính theo a thể tích V của khối chóp S.ABC?
A. V = a 6 3 4 .
B. V = a 6 3 6 .
C. V = a 3 2 .
D. V = a 6 3 12 .
Cho hình chóp S . A B C có đáy A B C là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng S B C là 6 4 , từ B đến mặt phẳng S A C là 15 10 ; từ C đến mặt phẳng S A B là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác A B C . Thể tích khối chóp S . A B C bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và SA=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B' và C'. Thể tích khối chóp S.A'B'C' bằng:
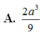
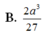
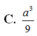
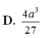
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a; ACB ^ = 60 o . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
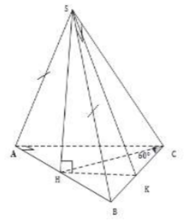
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16