Question

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, S A ⊥ A B C . Khẳng định nào dưới đây là sai?

A. S A ⊥ B C

B. S B ⊥ A C

C. S A ⊥ A B

D. S B ⊥ B C

Answer 1

Đáp án B.

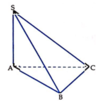
Ta có S A ⊥ ( A B C ) A B ⊂ ( A B C ) B C ⊂ ( A B C ) ⇒ S A ⊥ A B  và S A ⊥ B C . Vậy A, C đúng.

Do   Δ A B C vuông tại B nên B C ⊥ A B .

Ta có B C ⊥ S A , S A ⊂ S A B B C ⊥ A B , A B ⊂ S A B S A ∩ A B = A ⇒ B C ⊥ S A B , S B ⊂ S A B ⇒ B C ⊥ S B

Vậy B đúng.