Chọn C.
Phương pháp:
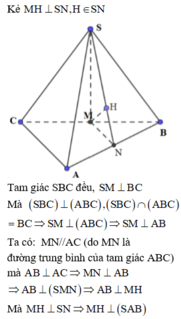
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.

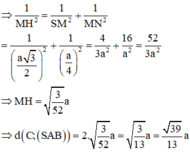
Chọn C.
Phương pháp:
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.


Cho hình chóp S.ABC có đáy là tam giác vuông tại A, ABC = 30 ° . Mặt bên SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ C đến mặt phẳng (SAB).
A. 39 a 13 .
B. 39 a 3 .
C. 26 a 13 .
D. 39 a 26 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , A B C ^ = 30 ° , tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).
A. h = 2 a 39 13
B. h = a 39 13
C. h = a 39 26
D. h = a 39 52
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A, ABC ^ = 30 0 tam giác SBC đều cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Tính khoảng cách từ A đến (SBC).
A. a 6
B. 3 a 14 7
C. a 2 3
D. 2 a 7
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A góc A B C ^ = 30 0 ; tam giác SBC là tam giác đều cạnh a và măt phẳng S A B ⊥ mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 6 5
B. a 6 3
C. a 3 3
D. a 6 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB=a và BAC= 30 ° Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC) Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) biết khối chóp S.ABC có thể tích bằng a 3 3 36
A. d = a 2 4
B. d = a 3
C. d = a 5 3
D. d = a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là 6 4 , từ B đến mặt phẳng (SAC) là 15 10 từ C đến mặt phẳng (SAB) là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC là
A. 2 a 2 .
B. a 2 .
C. 3 a 4 .
D. 3 a 2 .
Cho hình chóp S.ABC có đáy là ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng a 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (SBC):
A. d = 6 a 195 65
B. d = 4 a 195 195
C. d = 4 a 195 65
D. d = 8 a 195 195
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
A. a 22 11
B. a 4 3
C. a 11 22
D. a 3 4