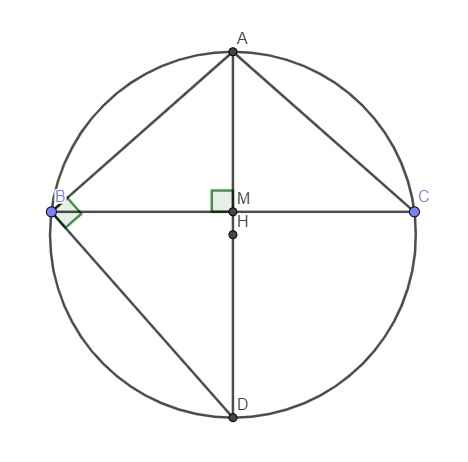
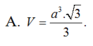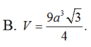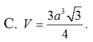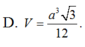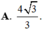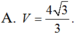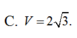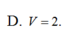Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
Gọi M là trung điểm BC, do tam giác cân tại A \(\Rightarrow H\in AM\)
Kéo dài AM cắt đường tròn ngoại tiếp tam giác tại D \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
\(BM=\dfrac{1}{2}BC=\dfrac{3a}{2}\) \(\Rightarrow AM=\sqrt{AB^2-BM^2}=\dfrac{a\sqrt{7}}{2}\)
Áp dụng hệ thức lượng:
\(AB^2=AM.AD\Rightarrow AD=\dfrac{AB^2}{AM}=\dfrac{8a\sqrt{7}}{7}\)
\(\Rightarrow AH=\dfrac{AD}{2}=\dfrac{4a\sqrt{7}}{7}\)
\(\Rightarrow SH=\sqrt{SA^2-AH^2}=\dfrac{2a\sqrt{21}}{7}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AM.BC=...\)