Các câu hỏi tương tự
Cho hình chóp S.ABC có
A
S
B
^
C
S
B
^
60
∘
,
A...
Đọc tiếp
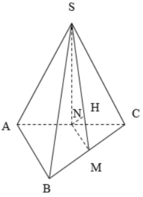
Cho hình chóp S.ABC có A S B ^ = C S B ^ = 60 ∘ , A S C ^ = 90 ∘ , S A = S B = S C = a . Tính khoảng cách d từ A đến mặt phẳng (SBC).
A. d = 2 a 6 .
B. d = a 6 .
C. d = 2 a 6 3 .
D. d = a 6 3 .
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng
60
°
,
S
A
a
,
S
B
2
a
,
S
C
3
a
. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC) A.
a
3
B.
a
6
C.
a
6
3...
Đọc tiếp
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 60 ° , S A = a , S B = 2 a , S C = 3 a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
A. a 3
B. a 6
C. a 6 3
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
. Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hình chóp là A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
A
C
a
3
,
B
C
2
a
.
Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Chiều cao SH của hìn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , A C = a 3 , B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Chiều cao SH của hình chóp là
A. a 15 5
B. a 15 3
C. 2 a 15
D. a 5 3
Trong không gian Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu
S : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ⏜ = 60 ° , B M C ⏜ = 90 ° , C M A ⏜ = 120 ° có dạng M (a;b;c) với a <0. Tổng a+b+c bằng:
A. 10 3 .
B. 2
C. - 2
D. 1
Cho hình chóp S.ABC có ASBCSB
60
°
và SASBSCa Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) A.
d
2
a
6
B.
d
a
6
3
C.
d
2
a
6
3
D.
d
a...
Đọc tiếp
Cho hình chóp S.ABC có ASB=CSB= 60 ° và SA=SB=SC=a Tính khoảng cách d từ điểm A đến mặt phẳng (SBC)
A. d = 2 a 6
B. d = a 6 3
C. d = 2 a 6 3
D. d = a 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là
6
4
, từ B đến mặt phẳng (SAC) là
15
10
từ C đến mặt phẳng (SAB) là
30
20
và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng A.
1...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng (SBC) là 6 4 , từ B đến mặt phẳng (SAC) là 15 10 từ C đến mặt phẳng (SAB) là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác ABC. Thể tích khối chóp S.ABC bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M có thể kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm ) thỏa mãn A M B ^ = 60 ° , B M C ^ = 90 ° ; C M A ^ = 120 ° có dạng M(a;b;c) với a<0. Giá trị T=a+b+c bằng:
A. T=1
B. T = 10 3
C. T=2
D. T=-2
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, ABADa, CD2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD Biết thể tích tứ diện SBCD bằng
a
3
6
. Tính khoảng cách từ A đến mặt phẳng (SBC) là: A.
a
3
2
B.
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, AB=AD=a, CD=2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD Biết thể tích tứ diện SBCD bằng a 3 6 . Tính khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 3 2
B. a 2 6
C. a 3 6
D. a 6 4
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Điểm M(a;b;c)(với a < 0) trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (S) ( A, B, C là các tiếp điểm) thõa mãn các góc A M B ^ = 60 ° , B M C ^ = 90 ° , C M A ^ = 120 ° . Tính abc bằng
A. 4
B. 10 3
C. -2
D. 2