Question

Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm SC. Tính góc phẳng nhịdiện [M, BD, A]?

Answer 1

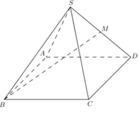
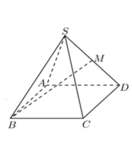
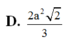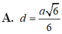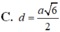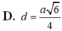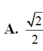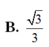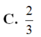Cho O là giao điểm giữa AC;BD 

Ta có SO vuông BD; AC vuông BD; SO;AC chứa (SAC) 

=> BD vuông (SAC) 

Ta có (SAC) giao (MBD) = MO 

(SAC) giao (ABD) = AO 

=> góc nhị diện  [M;BD;A] là số đo ^MOA 

Do tam giác SOC vuông tại O, M là trung điểm nên OM = SM = a/2 

Theo Pytago tam giác SOC vuông tại O 

\(SO=\sqrt{SC^2-OC^2}=\sqrt{a^2-\dfrac{2a^2}{4}}=\dfrac{\sqrt{2}}{2}a\)

cos^SOM = \(\dfrac{SO^2+OM^2-SM^2}{2.SO.OM}\)

=> ^SOM = 45⁰ 

=> [M;BD;A] = ^SOM + ^SOA = 135⁰