Các câu hỏi tương tự
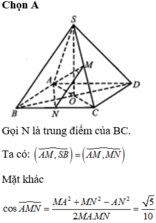
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, AD 3a, BC CD 4a; cạnh bên SA vuông góc với đáy và
S
A
a
3
. Gọi M là điểm nằm trên cạnh AD sao cho AM a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cosα bằng A.
5
5
B.
6
3
C.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, AD = 3a, BC = CD = 4a; cạnh bên SA vuông góc với đáy và S A = a 3 . Gọi M là điểm nằm trên cạnh AD sao cho AM = a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cosα bằng
A. 5 5
B. 6 3
C. 2 3
D. 6 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cosα bằng A.
3
6
B.
6
3
C.
2
3
D.
2
6
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cosα bằng
A. 3 6
B. 6 3
C. 2 3
D. 2 6
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của AD và SD. Số đo của góc giữa hai đường thẳng MN và SC. A.
45
0
B.
60
0
C.
30
0
D.
90
0
Đọc tiếp
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của AD và SD. Số đo của góc giữa hai đường thẳng MN và SC.
A. 45 0
B. 60 0
C. 30 0
D. 90 0
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi α là số đo của góc hợp bởi hai mặt phẳng (AB’C) và (BCC’B’). Khi đó cosα bằng A.
7
7
B.
2
7
7
C.
10
4
D.
3
4
Đọc tiếp
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi α là số đo của góc hợp bởi hai mặt phẳng (AB’C) và (BCC’B’). Khi đó cosα bằng
A. 7 7
B. 2 7 7
C. 10 4
D. 3 4
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a,
A
B
C
^
60
°
mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo gó giữa đường thẳng SB và mặt phẳng (SCD). Khi đó cosα bằng A.
1
4
B.
6
4
C.
3
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, A B C ^ = 60 ° mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo gó giữa đường thẳng SB và mặt phẳng (SCD). Khi đó cosα bằng
A. 1 4
B. 6 4
C. 3 2
D. 10 4
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA,
α
là góc tạo bởi đường thẳng EM và mặt phẳng
S
B
D
,
tan
α
bằng A.
2
B.
3
C. 2 D. 1
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E; M lần lượt là trung điểm của BC và SA. Gọi α là góc tạo bởi EM và (SBD). Khi đó tanα bằng: A. 1. B. 2. C.
2
D.
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E; M lần lượt là trung điểm của BC và SA. Gọi α là góc tạo bởi EM và (SBD). Khi đó tanα bằng:
A. 1.
B. 2.
C. 2
D. 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA,
α
là góc tạo bởi đường thẳng EM và mặt phẳng (SBD),
tan
α
bằng: A.
2
.
B.
3
C. 2 D. 1
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 2 .
B. 3
C. 2
D. 1
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3