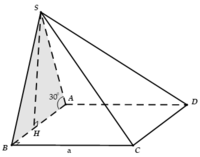
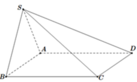
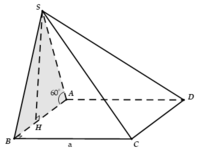
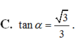Sửa đề: SA=2a
ABCD là hình vuông tâm O
nên OA=OB=OC=OD
S.ABCD là hình chóp đều
=>SA=SB=SC=SD
mà OA=OB=OC=OD
nên SO⊥(ABCD)
Kẻ OH⊥AB, OK⊥SH tại K
Ta có: AB⊥OH
AB⊥SO
OH,SO cùng thuộc mp(SOH)
Do đó: AB⊥(SOH)
=>AB⊥OK
Ta có: OK⊥SH
OK⊥AB
SH,AB cùng thuộc mp(SAB)
Do đó: OK⊥(SAB)
=>\(\hat{AO;\left(SAB\right)}=\hat{AO;AK}=\hat{OAK}\)
OK⊥(SAB)
=>OK⊥KA
=>ΔOKA vuông tại K
ABCD là hình vuông
=>\(AC^2=AB^2+BC^2=\left(2a\right)^2+\left(2a\right)^2=8a^2\)
=>\(AC=2a\sqrt2\)
=>\(OA=OC=OB=\frac{2a\sqrt2}{2}=a\sqrt2\)
ΔSOA vuông tại O
=>\(SO^2+OA^2=SA^2\)
=>\(SO^2=\left(2a\right)^2-\left(a\sqrt2\right)^2=4a^2-2a^2=2a^2\)
=>\(SO=a\sqrt2\)
Xét ΔDBO có OH//AD
nên \(\frac{OH}{AD}=\frac{BO}{BD}=\frac12\)
=>\(OH=\frac{AD}{2}=\frac{2a}{2}=a\)
Xét ΔSOH vuông tại O có OK là đường cao
nên \(\frac{1}{OK^2}=\frac{1}{OH^2}+\frac{1}{SO^2}=\frac{1}{\left(a\sqrt2\right)^2}+\frac{1}{a^2}=\frac{1}{2a^2}+\frac{1}{a^2}=\frac{3}{2a^2}\)
=>\(OK^2=\frac{2a^2}{3}\)
=>\(OK=a\sqrt{\frac23}=\frac{a\sqrt6}{3}\)
Xét ΔOKA vuông tại K có sin OAK=\(\frac{OK}{OA}=\frac{a\sqrt6}{3}:a\sqrt2=\frac{a\sqrt6}{3\cdot a\sqrt2}=\frac{\sqrt6}{3\sqrt2}=\frac{\sqrt3}{3}\)
nên \(\hat{OAK}\) ≃35 độ
=>\(\hat{AO;\left(SAB\right)}\) ≃35 độ