Các câu hỏi tương tự
Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó, diện tích của tam giác GKL bằng:
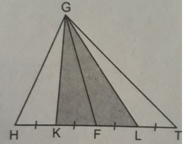
(A) 1/2 S;
(B) 1/4 S;
(C) 1/8 S;
(D) 3/4 S.
Cho hình bs.31, (R là điểm bất kì trên QS, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng:
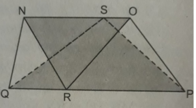
(A) 1/2 S; (B) 1/4 S;
(C) 3/4 S; (D) S
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJSABI+SCBJBài 3: Cho tam giác ABC có AB3cm, BC4cm, CA5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tí...
Đọc tiếp
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?
1) Cho hinh thoi ABCD, có S=12 cm vuông . Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD, DA . Tinh diệ tích MNPQ?
2) Cho hình binh hành có 1 cạnh bằng 2 cạnh kia . Biết cạnh bé bằng 5cm . Tính đường cao tương ứng với cạnh lớn . Biết diện tích bằng 50 cm vuông
3) Cho hinh Chử nhật là trung điểm của AB,BC,CD,DA . tính diện tích MNPQ
Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = 1/3 BC. Tính diện tích của tứ giác ABMD theo S
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.
Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S
Cho hình bình hành ABCD vẽ bốn điểm P,Q,R,S của các cạnh CD,AD,AB và BC. chứng minh tứ giác tạo bởi các dường thẳng này có diện tích bằng 1/5 dieenh tích hình bình hành ABCD
Mình có mấy bài toán bất đẳng thức hình họcBài 1:Cho hình vuông ABCD có đường chéo bằng 1.Tứ giác MNPQ nội tiếp ABCD(M,N,P,Q thứ tự thuộc AB,BC,CD,AD.CMR: chu vi MNPQ ko nhỏ hơn 1/2Bài 2:Tổng 2 cạnh đối trong tứ giác nhỏ hơn tông hai đg chéo của tứ giác đóBài 3:Cho tam giác ABC có các đg cao ha,hb,hc ứng vs các cạnh BC,AC,AB có độ dai tương ứng là a,b,c.CMR:Nếu ab thì a.hab.hb.dấu xảy ra khi nào?Bài 4:Cho M thuộc CD của hình vuông ABCD.tia phân giác góc ABM cắt cạnh AD tại I.CMR: BI 2MIBài 5:Ch...
Đọc tiếp
Mình có mấy bài toán bất đẳng thức hình học
Bài 1:Cho hình vuông ABCD có đường chéo bằng 1.Tứ giác MNPQ nội tiếp ABCD(M,N,P,Q thứ tự thuộc AB,BC,CD,AD.CMR: chu vi MNPQ ko nhỏ hơn 1/2
Bài 2:Tổng 2 cạnh đối trong tứ giác nhỏ hơn tông hai đg chéo của tứ giác đó
Bài 3:Cho tam giác ABC có các đg cao ha,hb,hc ứng vs các cạnh BC,AC,AB có độ dai tương ứng là a,b,c.CMR:Nếu a>b thì a.ha>=b.hb.dấu '=' xảy ra khi nào?
Bài 4:Cho M thuộc CD của hình vuông ABCD.tia phân giác góc ABM cắt cạnh AD tại I.CMR: BI<= 2MI
Bài 5:Cho tứ giác có diện tích là S và bốn cạnh a,b,c,d.Cmr: 4S<=a^2+b^2+c^2+d^2