Các câu hỏi tương tự
Cho hình bs.31, (R là điểm bất kì trên QS, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng:
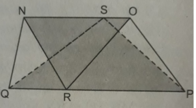
(A) 1/2 S; (B) 1/4 S;
(C) 3/4 S; (D) S
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng:
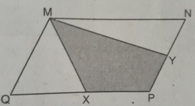
(A) 1/4 S;
(B) 1/2 S;
(C) 1/8 S;
(D) 3/4 S.
Trong 1 hình tròn có diện tích S lấy 2017 điểm bất kì. C/m ít nhất có 3 điểm tạo thành 1 tam giác mà diện tích S< S/1008
Cho hình thang ABCD (AB//CD) và O là giao 2 đường chéo AC và BD. CMR:
a)S tam giác AOD= S tam giác BOC.
b)Tích của diện tích tam giác AOB và diện tích tam giác COD bằng bình phương diện tích tam giác BOC.
Hộ mk nka. Chi tiết 1 chút !!! ;)
Cho một hình ngũ giác có ba đường thẳng d1,d2,d3 cắt nhau tại 3 điểm A,B,C thuộc miền trong ngũ giác sao cho 1 đường thẳng chia ngũ giác thành 2 phần co diện tích bằng nhau. Chứng minh rằng: S của ABC<1/4 S của ngũ giác đã cho
Cho một hình ngũ giác có ba đường thẳng d1,d2,d3 cắt nhau tại 3 điểm A,B,C thuộc miền trong ngũ giác sao cho 1 đường thẳng chia ngũ giác thành 2 phần co diện tích bằng nhau. Chứng minh rằng: S của ABC<1/4 S của ngũ giác đã cho
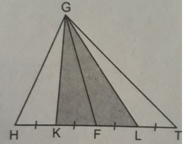
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJSABI+SCBJBài 3: Cho tam giác ABC có AB3cm, BC4cm, CA5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tí...
Đọc tiếp
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?
Gọi a,b,c,d theo thứ tự là độ dài các cạnh AB,BC,CD,DA của tứ giác ABCD , S và p theo thứ tự là diện tích và nửa chu vi của tứ giác đó a CMR S<= 1/2(ab+cd) b. CMR 4S<= (a+c)(b+d)<=p^2 c. CMR S<= a^2+b^2+c^2+d^2/4
1.Chứng minh nếu 1 hình bình hành và tam giác có cùng cạnh đáy và chiều cao thì diện tích hình bình hành bằng 2 lần diện tích tam giác
2. Cho hình bình hành ABCD, O nằm trong hình bình hành. chứng minh SAOB +SCOD=SAOD + SBOC