a) Ta có: AE = CG (giả thiết) mà AB = CD (cạnh đối của hình bình hành ABCD), suy ra BE = DG.
△BEF và △DGH có:
BE = DG (chứng minh trên)
B^=D^ (hai góc đối của hình bình hành ABCD)
do đó: △BEF = △DGH (c.g.c), suy ra EF = GH.
Chứng minh tương tự, ta có: EH = FG.
Tứ giác EFGH có các cạnh đối bằng nhau nên là hình bình hành.
b) Tứ giác ABCD là hình bình hành ...
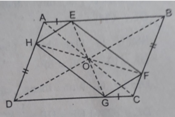
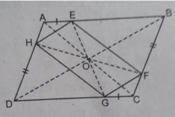
Cho hình bình hành ABCD tên các cạnh AB, BC, CD, DA lấy tương ứng các điểm E, F, G, H sao cho AE = CG; BF = DH. CMR:
a, EFGH là hình bình hành
b, Các đường thẳng AC; BD; EG; HF cắt nhau tại 1 điểm
a) Ta có: AE = CG (giả thiết) mà AB = CD (cạnh đối của hình bình hành ABCD), suy ra BE = DG.
△BEF và △DGH có:
BE = DG (chứng minh trên)
B^=D^ (hai góc đối của hình bình hành ABCD)
do đó: △BEF = △DGH (c.g.c), suy ra EF = GH.
Chứng minh tương tự, ta có: EH = FG.
Tứ giác EFGH có các cạnh đối bằng nhau nên là hình bình hành.
b) Tứ giác ABCD là hình bình hành ...
đúng không