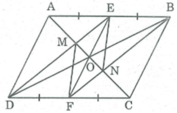
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB và CD.Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh tứ giác EMFN là hình bình hành.
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
Cho hình bình hành ABCD có E,F theo thứ tự là trung điểm của AB và CD.
a, Tứ giác DEBF là hình gì?Vì sao
b, Chứng minh rằng các đường thẳng AC,BD,È cùng cắt nhau tại một điểm.
c,Gọi giao điểm của AC với DE và Bf theo thứ tự là M và N.Chứng minh rằng tứ giác EMFN là hình bình hành.
Hình bình hành:
1. Cho tứ giác ABC, gọi E, F là trung điểm của AB và CD; M, N, P, Q lần lượt là trung điểm các đoạn AF, CE, BF và DE. C Chứng minh rằng MNPQ là hình bình hành.
2. Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a. M, N theo thứ tự là trung điểm của CD, AB.
b. EMFN là hình bình hành.
Cho hình hành ABCD có E,F lần lượt là trung điểm của AB,CD. gọi giao điểm của AC với DE và BF theo thứ tự M và N
chứng minh EMFN là hình bình hành
Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB và CD.
a. Tứ giác DEBF là hình gì ? Vì sao ?
b. Chứng minh 3 đường thẳng AC, BD, EF đồng quy
c. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh tứ giác EMFN là hình bình hành.
cho hình bình hành ABCD có AB=2AD.Gọi E và F theo thứ tự là trung điểm của AB và CD.
a.Các tứ giác AEFD,AECF là hình gì?vì sao?
b.Gọi M là giao điểm của AF và DE,gọi N là giao điểm của BF và CE.Chứng minh rằng tứ giác EMFN là hình chữ nhật
c.Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông
cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD; N là giao điểm của DE và AB. Chứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD, AB.
b) EMFN là hình bình hành.
cho hình bình hành ABCD, gọi E,F lần lượt là trung điểm của AB và CD
a, Tứ giác DEBF là hình gì?
b, Chứng minh ba đường thẳng AC,BD,EF đồng quy
c, Gọi giao điểm của AC với DE và BF theo thứ tự tại M và N. Chứng minh tứ giác EMFN là hình bình hành
