Các câu hỏi tương tự
cho hình bình hành ABCD có đường chéo AC là lớn nhất .từ C hạ các đường vuông góc CE và CF lần lượt xuống các tia AB,AD .chứng minh rằng AB.AE+AD.AF=AC2
Cho hình bình hành ABCD có Ac là đường chéo lớn. Từ C kẻ CE vuông góc với đường thẳng Ab (E\(\in\)AB) và kẻ CF vuông góc với đường thẳng AD (F\(\in\)AD). Chứng minh \(AB.AE+AD.AF=AC^2\)
Cho hình bình hành ABCD có AC BD. Kẻ
C
E
⊥
A
B
tại E,
C
F
⊥
A
D
tại F,
B
H
⊥
A
C
tại H và
D
K
⊥
A
C
tại K. Chứng minha)
A
B
A
C
A
H...
Đọc tiếp
Cho hình bình hành ABCD có AC > BD. Kẻ C E ⊥ A B tại E, C F ⊥ A D tại F, B H ⊥ A C tại H và D K ⊥ A C tại K. Chứng minh
a) A B A C = A H A E ;
b) A D . A F = A K . A C ;
c) A D . A F + A B . A E = A C 2 .
Cho hình bình hành ABCD ( AB > AD) Từ C kẻ CE và CF vuông góc với đường thẳng AB , AD ( E thuộc AB , F thuộc AD) . Chứng minh
AB.AE + AD.AF = AC^2
Cho hình bình hành ABCD với AC là đường chéo lớn. Kẻ CE vuông góc AB; CF vuông góc AD; BH vuông góc AC.
Chứng minh : a) t.giác AEC đồng dạng t.giác AHB.
b) AD.AF = CA.CH.
c) AB.AE + AD.AF= AC^2
Cho hình bình hành ABCD. Kẻ CE vuông góc với đg thẳng AB tại E, kẻ CF vuông góc với đg thẳng AD tại F. CM: AC2 = AB.AE+AD.AF
Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với AB và CF vuông góc với AD. Chứng minh AB.AE + AD.AF = AC^2
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF
A
C
2
Đọc tiếp
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF = A C 2
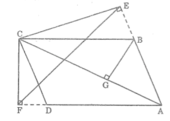
Cho hình bình hành ABCD (AB > AD). Từ C vẽ CE, CF lần lượt vuông góc với các đường thẳng AB, AD (E thuộc AB, F thuộc AD). Chứng minh rằng AB.AE + AD.AF = AC2.









