ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AB//CD
=>góc OAB=góc OCD
mà góc OAB=góc ODC
nên góc ODC=góc OCD
=>OC=OD
=>AC=BD
Xét hình bình hành ABCD có AC=BD
nên ABCD là hình chữ nhật
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AB//CD
=>góc OAB=góc OCD
mà góc OAB=góc ODC
nên góc ODC=góc OCD
=>OC=OD
=>AC=BD
Xét hình bình hành ABCD có AC=BD
nên ABCD là hình chữ nhật
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.
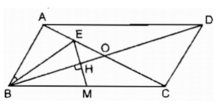
Cho hình bình hành ABCD , O là giao điểm của hai đường chéo, H là hình chiếu của A trên OD . Biết rằng các góc DAH ; HAO ; OAB bằng nhau . Chứng minh ABCD là hình chữ nhật.
Cho hình chữ nhật ABCD. Các đường chéo AC, BD cắt nhau tại O. Chứng minh 4 tam giác OAB,OBC,OCD,OAD có diện tích bằng nhau.
Cho hình bình hành ABCD,O là giao điểm của hai đường chéo. AH vuông góc BD .Biết các góc DAH;HAO;OAB bằng nhau.CMR ABCD là hình chữ nhật.
Cho hình bình hành ABCD. Các đường phân giác của các góc lần lượt cắt nhau tại E, F, G, H. Chứng minh:
a) EFGH là hình chữ nhật
b) Đường chéo của hình chữ nhật EFGH song song với cạnh hình bình hành ABCD
cho hình bình hành ABCD, có đường chéo AC>BD cắt nhau tại O,kẻ BE vuông góc với AC,DF vuông góc với AC,
a chứng minh tứ giác BEDF là hình bình hành
b gọi H,K lần lượt là hình chiếu của C trên các đường thằng AB,CD.CHúng minh rằng CH.CD=CB.CK
c chứng minh AB.AH+AD.AK=AC2
Cho hình bình hành ABCD, 2 đường chéo cắt nhau tại O. Kẻ AH vuông góc BD, CD vuông góc BD (AC ko vuông góc BD)
a) C/m tứ giác AHCK là hình bình hành
b)Biết AH cắt CD tại M, CK cắt AB tại N. C/m O là trung điểm của MN
Cho hình bình hành ABCD,, phân giác góc A cắt đường chéo BD tại E và phân giác góc B cắt đường chéo AC tại F. Chứng minh rằng EF // AB.
1,Cho hình thang ABCD,2 cạnh đáy AB và CD.2 đường chéo cắt nhau tại O.biết rằng OA=2cm,OC=6cm,OB=4cm.OD?
2,cho hình bình hành ABCD.Cac điểm M,N lần lượt thuộc cạnh AB và CD sao cho AM=CN.Chứng minh
a,AMCN là hình bình hành
b,3 đường thẳng AC,BD,MN đồng quy
3.Cho tứ giác ABCD có AB vuông góc với BD,AC vuông góc với CD.2 đường chéo cắt nhau tại I.chứng minh IA.IC=IB.ID