Ta có:
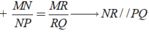
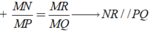
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
Ta có:
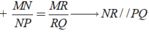
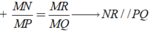
Cả 3 đáp án A, B, C đều sai.
Chọn đáp án D.
cho Δ ABC vuông tại A.M,N,P lần lược là trung đ của AB,AC,BC.
a) c/m rằng tứ giác BMNP là hình bình hanh
b) c/m rằng tứ giác AMPN là hình chữ nhật
c) vẽ Q đối xứng vs P qua N,R đối xứng vs P qua M.c/m rằng R,A,Q thẳng hàng
Cho tam giác ABC vuông tại A , M N P lần lượt là trung điểm của AB AC BC
a Chứng minh tứ giác bmnc là hình bình hành
b cm AMPN là hcn
c vẽ Q dx P qua N ,R dx P qua M, CM R,A,Q thẳng hàng
d BN cắt QC tại K cm QK =1/2KC
Vẽ Q đối xứng với P qua N, R đối xứng với P qua M. Chứng minh rằng R,A,Q
thẳng hàng
Cho tam giác ABC có A=90 . Gọi M , N , P lần lượt là trung điểm của AB , AC , BC
Chứng minh rằng :
a) BMNP là hình bình hành
b) AMPN là hình chữ nhật
c) Gọi Q là điểm đối xứng của P qua N , R là điểm đối xứng của P qua M
Chứng minh R ,A , Q thẳng hàng
Cho hai đa thức P(x) =x4+5x3-4x2+3x+m; Q(x)=x4+4x3-3x2+2x+n
a) Tìm m,n để P(x) ,Q(x) chia hết cho (x-2)
b)Xét đa thức R(x)=P(x)-Q(x). Với giá trị m,n vừa tìm chứng tỏ rằng đa thức R(x) chỉ có duy nhất 1 nghiệm
Cho tam giác ABC vuông tại A. Gọi M,N,P lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh rằng : Tứ giác BMNP là hình bình hành
b) Vẽ Q đối xứng với P qua N, R đối xứng với P qua M. Chứng minh rằng R,A,Q
thẳng hàng
Cho hình thang ABCD (AB//CD). Gọi M ,N, P, Q R lần lượt là trung điểm AD, BC ,AC, BD. Chứng minh M,N,P,Q thẳng hàng .Nếu AB bằng 7 cm,CD=3 .Tính MN,PQ
Cho hình thang ABCD (AB//CD). Gọi M ,N, P, Q R lần lượt là trung điểm AD, BC ,AC, BD. Chứng minh M,N,P,Q thẳng hàng .Nếu AB bằng 7 cm,CD=3 .Tính MN,PQ
Cho hai đa thức: \(P\left(x\right)=x^4+5x^3-4x^2+3x+m\)và \(Q\left(x\right)=x^4+4x^3-3x^2+2x+n\)
a) Tìm giá trị của m,n để các đa thức P(x) và Q(x) chia hết cho ( x -2 )
b) Xét đa thức R(x) = P(x) - Q(x) với giá trị m,n vừa tìm được. Hãy chứng tỏ rằng đa thức R(x) chỉ có một nghiệm duy nhất.
Cho tứ giác MNPQ bik góc M : N : P : Q=1 : 2 : 3 : 4
a) Tính góc M, N, P, Q.
b) Cm: MN//PQ
c) Gọi R là giao điểm của MQ và NP. Tính các góc của tam giác PQR