Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1
Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1
Cho hàm số y = f(x)(x - 1) xác định và liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = f x x − 1 cắt đồ thị hàm số tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
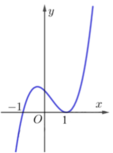
A. m > 0.
B. m > 1 m < 0 .
C. m < 1.
D. 0 < m < 1.
Cho hàm số y = f ( x ) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 2 m - 1 cắt đồ thị (C) tại 2 điểm phân biệt
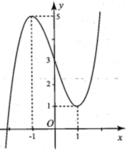
A. m > 3
B. m < 1
C. m = 1 m = 3
D. 1 < m < 3
Cho hàm số y = f ( x ) liên tục trên ℝ có đồ thị ( C ) như hình vẽ dưới đây :
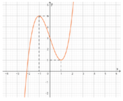
Tìm tất cả các giá trị thực của tham số m để đường thẳng y=2m-1 1cắt đồ thị ( C ) tại hai điểm phân biệt.
A. m = - 5 m = 1
B. m > 3
C. 1 < m < 3
D. m = 3 m = 1
Cho hàm số y=f(x) xác định và liên tục trên các khoảng ( - ∞ ; 0 ) , ( 0 ; + ∞ ) và có bảng biến thiên như sau
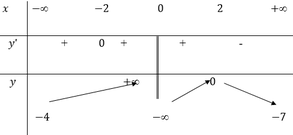
Tìm tất cả các giá trị thực của m để đường thẳng y=m cắt đổ thị hàm số y=f(x) tại 3 điểm phân biệt
A. - 4 ≤ m < 0
B. - 4 < m < 0
C. - 7 < m < 0
D. - 4 < m ≤ 0
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ . Hàm số y=f '(x) có đồ thị như hình vẽ bên dưới. Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số g x = 2 f 2 x + 3 f x + m có đúng 7 điểm cực trị, biết f a = 1 , f b = 0 , lim x → + ∞ f x = + ∞ , lim x → − ∞ f x = − ∞
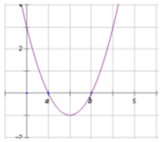
A. S = − 5 ; 0
B. S = − 8 ; 0
C. S = − 8 ; 1 6
D. S = − 5 ; 9 8
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sinx+1)=m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là

A. (-2;0]
B. (0;2]
C. [-2;2]
D. (-2;0)
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình vẽ. Tìm tất cả các giá trị thực của tham số m để phương trình f ( x ) + m - 2019 = 0 có ba nghiệm phân biệt.
A.m < 2016, m > 2020
B. 2016 < m < 2020
C. m ≤ 2016 , m ≥ 2020
D. m = 2016, m = 2020
Cho hàm số y=f(x) xác định trên R và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)+m-2018=0 có duy nhất một nghiệm.
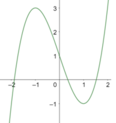
A. m ≤ 2015 , m ≥ 2019 .
B.2015<m<2019
C.m=2015,m=2019
D.m<2015,m>2019
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ bên và có đạo hàm f'(x) liên tục trên khoảng (-∞;+∞).Đường thẳng ở hình vẽ bên là tiếp tuyến của (C) tại điểm có hoành độ x=0. Gọi m là giá trị nhỏ nhất của hàm số y=f'(x). Mệnh đề nào dưới đây đúng ?
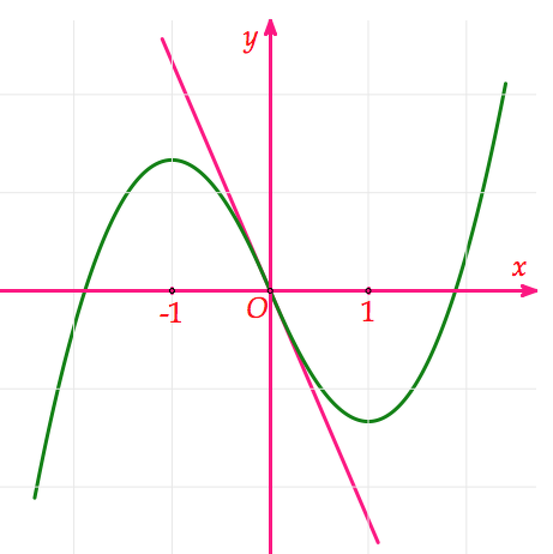
A. m < -2
B. -2 < m < 0.
C. 0 < m < 2
D. m > 2