Chọn D.
Dựa vào đồ thị ta thấy f(1,5)>0 và f(2,5)<0.
Chọn D.
Dựa vào đồ thị ta thấy f(1,5)>0 và f(2,5)<0.
Cho hàm số y=f(x) xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Gọi m là số nghiệm thực của phương trình f(f(x))=0 Khẳng định nào sau đây là đúng?

A. m=5
B. m=6
C. m=7
D. m=8
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số y = f x = x + 1 k h i x < 0 x 2 - 3 x + 1 k h i x ≥ 0 . Biết rằng hàm số y = f ( x ) có đồ thị (C) như hình vẽ bên. Khẳng định nào sau đây là sai?
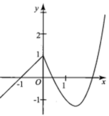
A. Hàm số đã cho không có đạo hàm tại điểm x = 0
B. Hàm số đã cho có 2 điểm cực trị
C. Hàm số đã cho liên tục trên R
D. Hàm số đã cho đồng biến trên R
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:
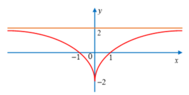
Trong các khẳng định sau:
I. Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2
II. Hàm số đạt cực tiểu tại x = -2
III. Hàm số nghịch biến trong khoảng − ∞ ; 0 và đồng biến trong khoảng 0 ; ∞
IV. Phương trình f(x) = m có hai nghiệm phân biệt khi và chỉ khi . Có bao nhiêu khẳng định đúng
A. 1
B. 2
C. 3
D. 4
Cho hàm số f (x) có đồ thị của hàm số f'(x) như hình vẽ bên.
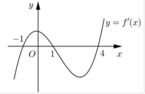
Biết f(-1)=f(4)=0. Hàm số y = ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
A. (-1;0).
B. (1;4).
C. ( - ∞ ; 1 ) .
D. ( 4 ; + ∞ ) .
Cho hàm số f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên và f(-2)=f(2)=0. Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
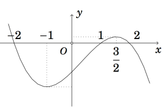
A. (1;2).
B. (-2;-1).
C. ( 5 ; + ∞ ) .
D. (2;5).
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ bên
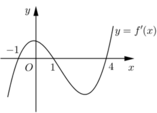
Biết f - 1 = f 4 = 0 . Hàm số y = f x 2 nghịch biến trên khoảng nào dưới đây ?
A. (-1;0)
B. (1;4)
C. - ∞ ; 1
D. 4 ; + ∞
Cho hàm số y = f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên. Biết f(-2)<0. Hàm số y = f 1 - x 2018 đồng biến trên khoảng nào dưới đây?
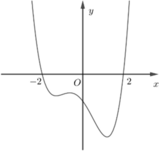
A. - 3 2018 ; 3 2018
B. - 1 ; + ∞
C. - ∞ ; - 3 2018
D. - 3 2018 ; 0
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ bên và có đạo hàm f'(x) liên tục trên khoảng (-∞;+∞).Đường thẳng ở hình vẽ bên là tiếp tuyến của (C) tại điểm có hoành độ x=0. Gọi m là giá trị nhỏ nhất của hàm số y=f'(x). Mệnh đề nào dưới đây đúng ?
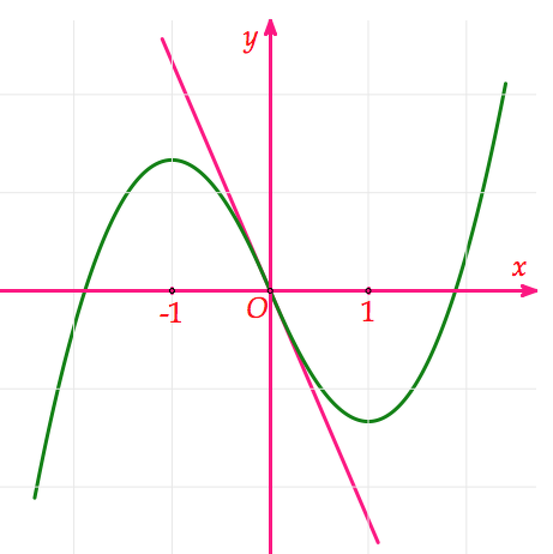
A. m < -2
B. -2 < m < 0.
C. 0 < m < 2
D. m > 2