Ta có
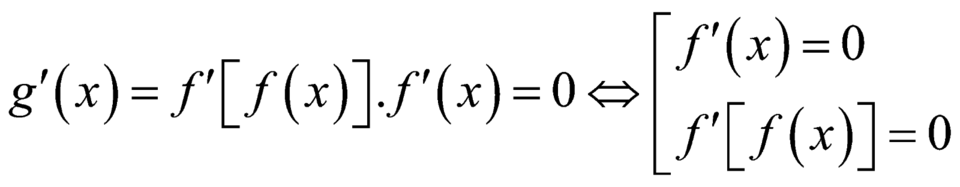
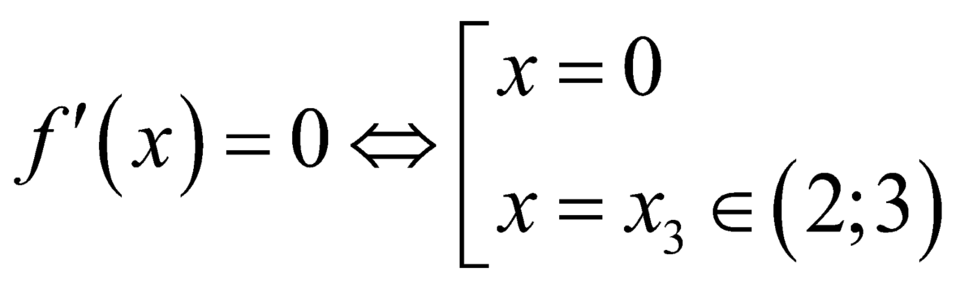
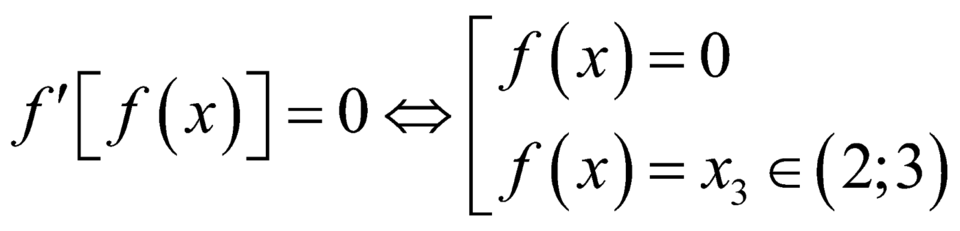
+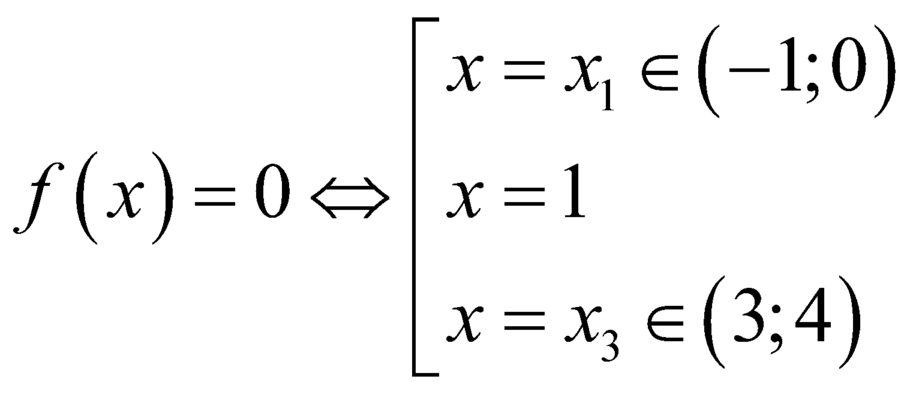
+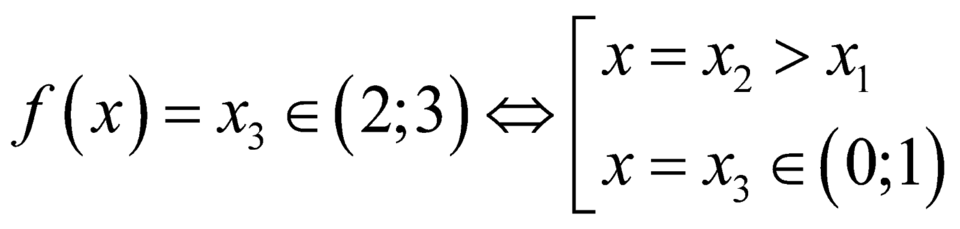 .
.
Vậy phương trình ![]() có 8 nghiệm phân biệt.
có 8 nghiệm phân biệt.
Đáp án D
Ta có
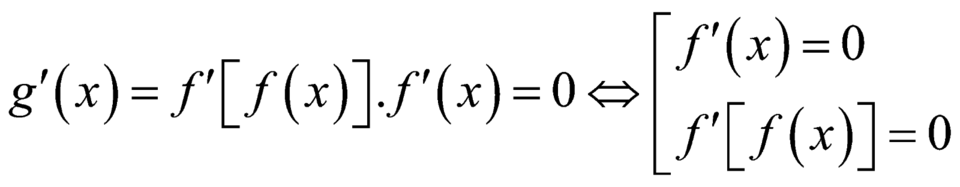
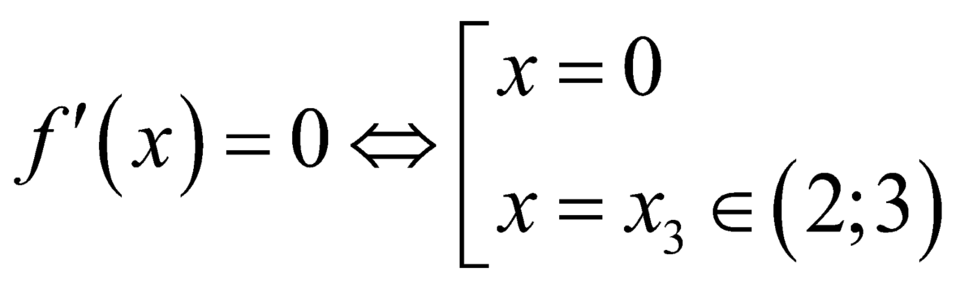
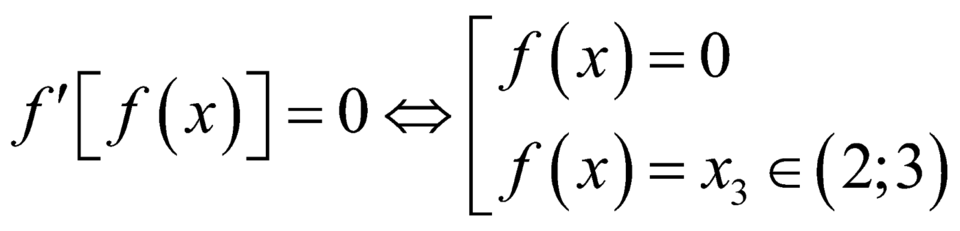
+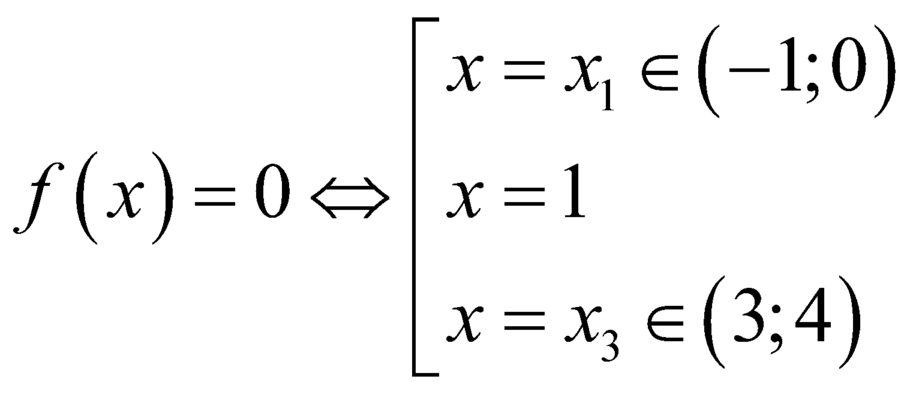
+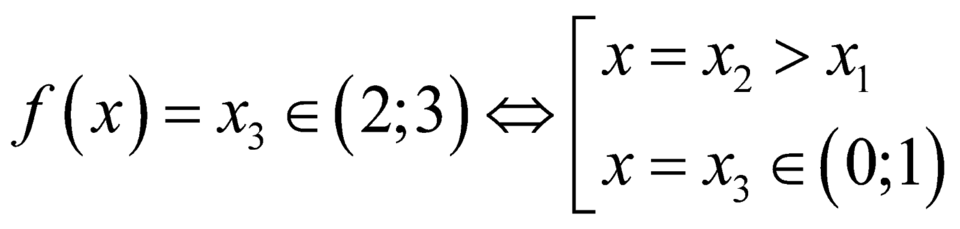 .
.
Vậy phương trình ![]() có 8 nghiệm phân biệt.
có 8 nghiệm phân biệt.
Đáp án D
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt g x = f x 2 Tìm số nghiệm của phương trình g'(x)=0

A. 5
B. 4
C. 3
D. 2
Cho hàm số y=f(x) có đạo hàm trên ℝ và có đồ thị là đường cong trong hình vẽ dưới. Đặt g(x) = f[f(x)]. Tìm số nghiệm của phương trình g'(x)=0
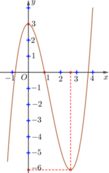
A. 2
B. 8
C. 4
D. 6
Cho hàm số y = f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x), (y = f’(x) liên tục trên R). Xét hàm số g(x) = f(x2 - 2). Mệnh đề nào dưới đây sai?

A. Hàm số g(x) nghịch biến trên (-∞;-3)
B. Hàm số g(x) có 3 điểm cực trị
C. Hàm số g(x) nghịch biến trên (-1;0)
D. Điểm cực đại của hàm số là 0
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị như hình vẽ
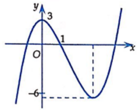
Đặt g x = 2 f x − 3 f x . Tìm số nghiệm của phương trình g’(x)=0
A. 5
B. 3
C. 2
D. 6
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Hàm số y= f'(x) có đồ thị như hình vẽ bên dưới:
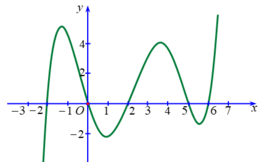
Số nghiệm thuộc đoạn [-2;6] của phương trình f(x) = f(0) là
A. 5
B. 2
C. 3
D. 4
Cho hàm số y= f(x) có đạo hàm trên R. Đường cong trong hình vẽ dưới là đồ thị của hàm số y= f’(x) . Xét hàm số g( x) = f( 3-x2).
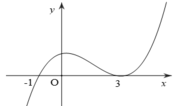
Mệnh đề nào dưới đây là đúng?
A. Hàm số y= g( x) đồng biến trên
B. Hàm số y= g( x) đồng biến trên (0 ;3)
C. Hàm số y= g(x) nghịch biến trên
D. Hàm số y= g(x) nghịch biến trên ![]() và (0;2)
và (0;2)
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
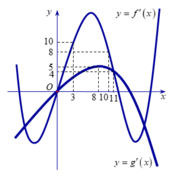
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong hình bên. Hàm số g(x) = f (3x - 2) nghịch biến trên khoảng
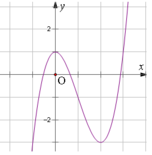
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y=f(x) có đạo hàm xác định trên tập r/{0} và đồ thị hàm số y=f(x) như hình vẽ bên dưới.
Có bao nhiêu giá trị nguyên của tham số m để phương trình
f
(
cos
2
x
)
=
m
có nghiệm?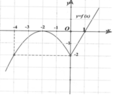
![]()
![]()
![]()
![]()