Chọn A.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (-∞;-1) và (0;1)
Chọn A.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (-∞;-1) và (0;1)
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. (1;+∞)
B.(-1;0)
C. (-∞;1)
D.(0;1)
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng

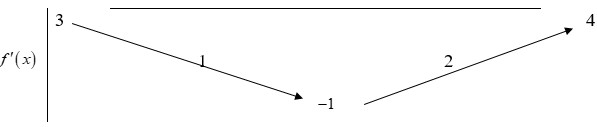
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y = f '(x) được cho như hình vẽ bên. Hàm số y = f 1 − x 2 + x nghịch biến trên khoảng
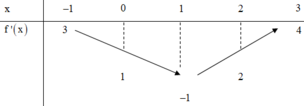
A. (2;4)
B. (-4;-2)
C. (-2;0)
D. (0;2)
Cho hàm số f(x) có đạo hàm liên tục trên ℝ . Bảng biến thiên của hàm số f’(x) trên đoạn [-1;3] như hình
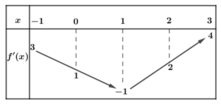
Hàm số g x = f 1 - x 2 + x nghịch biến trên khoảng nào trong các khoảng sau ?
A. (-4;-2)
B. (-2;0)
C. (0;2)
D. (2;4)
Cho hàm số y = f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như hình bên. Hàm số y = log x f 2 x đồng biến trên khoảng

A. (1;2)
B. - ∞ ; - 1
C. (-1;0)
D. (-1;1)
Cho hàm số y=f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như dưới đây

Hàm số y = log 2 f 2 x đồng biến trên khoảng
A. (1;2)
B. - ∞ ; - 1
C. (-1;0)
D. (-1;1)
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu của hàm số f'(x) như sau:

Hàm số y=f(x) đồng biến trên khoảng nào dưới đây ?
A.(0;2)
B. 1 ; + ∞
C. 0 ; + ∞
D. - ∞ ; 0
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:
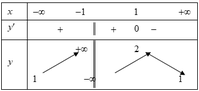
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có 3 tiệm cận.
B. Phương trình f(x) = m có 3 nghiệm thực phân biệt thì m ∈ 1 ; 2
C. Giá trị lớn nhất của hàm số là 2
D. Hàm số đồng biến trên - ∞ ; 1
Cho hàm số y=f(x) xác định trên R∖{1}, liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:
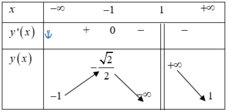
Khẳng định nào sau đây là đúng?
A. Giá trị lớn nhất của hàm số là −22
B. Đồ thị hàm số có 3 đường tiệm cận
C. Đồ thị hàm số có 2 giá trị cực tiểu
D. Hàm số nghịch biến trên khoảng (−1;+∞)