Các câu hỏi tương tự
Cho hàm số f(x)
2
x
+
m
x
+
1
với m là tham số thực. Tìm tất cả các giá trị của m 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3. A. 1m 3 B. m
∈
(
1
;
3
5
-
4
)
C....
Đọc tiếp
Cho hàm số f(x) = 2 x + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
A. 1<m< 3
B. m ∈ ( 1 ; 3 5 - 4 )
C. m ∈ ( 1 ; 5 )
D. 1<m≤ 4
Cho hàm số f(x)
x
-
m
2
+
m
x
+
1
với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2. A. m 1 B. m -2 C. m -1 D. m -1 hoặc m 2
Đọc tiếp
Cho hàm số f(x) = x - m 2 + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.
A. m= 1
B. m= -2
C. m= -1
D. m= -1 hoặc m= 2
Cho hàm số y
x
3
-
3
x
+
m
2
. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là A. 1 B. -4 C. 0 D. 4
Đọc tiếp
Cho hàm số y = x 3 - 3 x + m 2 . Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là
A. 1
B. -4
C. 0
D. 4
Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y
x
2
-
2
x
+
m
trên đoạn [-1; 2] bằng 5. A. -4 B. 2 C. 0 D . -2
Đọc tiếp
Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = x 2 - 2 x + m trên đoạn [-1; 2] bằng 5.
A. -4
B. 2
C. 0
D . -2
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số
y
x
2
-
3
x
+
m
trên đoạn [ 0; 2] bằng 3. Số phần tử của S là A. 1 B. 2 C. 3 D. 5
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 2 - 3 x + m trên đoạn [ 0; 2] bằng 3. Số phần tử của S là
A. 1
B. 2
C. 3
D. 5
Cho hàm số y x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m 0 , để giá trị nhỏ nhất của hàm số trên D [m+ 1; m+ 2] luôn bé hơn 3 là: A. (0; 1) B. (
1
2
; 1) C. (2; 3) D. (0; 2)
Đọc tiếp
Cho hàm số y= x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m> 0 , để giá trị nhỏ nhất của hàm số trên D= [m+ 1; m+ 2] luôn bé hơn 3 là:
A. (0; 1)
B. ( 1 2 ; 1)
C. (2; 3)
D. (0; 2)
Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số y
-
x
3
-
3
x
2
+
m
trên đoạn [-1;1] bằng 0. A. m 0. B. m 6. C. m 2. D. m 4.
Đọc tiếp
Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số y = - x 3 - 3 x 2 + m trên đoạn [-1;1] bằng 0.
A. m = 0.
B. m = 6.
C. m = 2.
D. m = 4.
Cho hàm số f(x) có đồ thị của hàm số f(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là A. m f(4), M f(1) B. m f(4), M f(2) C. m f(1), M f(2) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
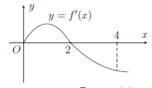
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị




