Đáp án C
Ta có y ' = 3 x 2 − 6 x = 0 ⇔ x = 0 ⇒ y = − 2 = a x = 2 ⇒ y = − 6 = b
Khi đó 2 a 2 + b = 2
Đáp án C
Ta có y ' = 3 x 2 − 6 x = 0 ⇔ x = 0 ⇒ y = − 2 = a x = 2 ⇒ y = − 6 = b
Khi đó 2 a 2 + b = 2
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Gọi M,n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y = x 2 + 3 x + 3 x + 2 . Khi đó giá trị của biểu thức M 2 − 2 n bằng
A.7
B.9
C.8
D.6
Gọi y C D , y C T lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số y = x 2 + 3 x + 3 x + 2 . Gía trị của biểu thức y C D 2 - 2 y C T 2 bằng
A. 9
B. 6
C. 8
D. 7
Hàm số y = a x 4 + b x 2 + c đạt cực đại tại A(0;-3) và đạt cực tiểu tại B(-1;-5). Khi đó, giá trị của a, b, c lần lượt là:
A. 2;4;-3
B. -3;-1;-5
C. -2;4;-3
D. 2;-4;-3
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Tìm số mệnh đề sai trong những mệnh đề sau
(1). Nếu hàm số f x đạt cực đại tại x0 thì x0 được gọi là điểm cực đại của hàm số.
(2). Giá trị cực đại (giá trị cực tiểu) của hàm số còn được gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
(3). Cho hàm số f x là hàm số bậc 3, nếu hàm số có cực trị thì đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt.
(4). Cho hàm số f x là hàm số bậc 3, nếu hàm số cắt trục Ox tại duy nhất một điểm thì hàm số không có cực trị.
A. 2
B. 3
C. 1
D. 4
Cho hàm số y=f(x) có bảng biến thiên như sau:
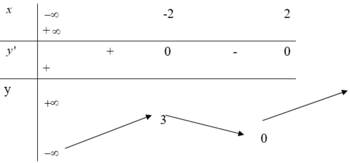
Giá trị cực đại và giá trị cực tiểu của hàm số đã cho lần lượt là?
A. 3 và -2
B. 2 và 0
C. -2 và 2
D. 3 và 0
Cho hàm số y = f x có đạo hàm trên đoạn a ; b . Ta xét các khẳng định sau:
(1) Nếu hàm số f x đạt cực đại tại điểm x 0 ∈ a ; b thì f x 0 là giá trị lớn nhất của f x trên đoạn a ; b .
(2) Nếu hàm số f x đạt cực đại tại điểm x 0 ∈ a ; b thì f x 0 là giá trị nhỏ nhất của f x trên đoạn a ; b
(3) Nếu hàm số f x đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 ( x 0 , x 1 ∈ a ; b ) thì ta luôn có f x 0 > f x 1 .
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3