Ta có
y ' = π x ' . x π + π x . x π ' = π x . x π - 1 π + xln π
Đáp án C
Ta có
y ' = π x ' . x π + π x . x π ' = π x . x π - 1 π + xln π
Đáp án C
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
A. f ( π ) = 0
B. f ( π ) = - π
C. f ( π ) = 4 π
D. f ( π ) = 2 π
Cho hàm số y = sin2 x+2 sinx, với x∈ [ - π ; π ] . Hàm số này có mấy điểm cực trị
A. Bốn.
B. Một.
C. Ba.
D. Hai.
Số điểm cực trị của hàm số y = sin x - π 4 ; x ∈ - π ; π là:
A. 2
B. 4
C. 3
D. 5
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số f(x) thỏa mãn ∫ 0 π f ' ( x ) d x = 1 , f ( 0 ) = π . Tính f ( π )
A. f ( π ) = 1 - π
B. f ( π ) = π - 1
C. f π = π + 1
D. f π = - π - 1
Cho hàm số y = f(x) là hàm số chẵn và liên tục trên đoạn - π ; π thỏa mãn ∫ 0 π f x d x = 2018 . Tích phân ∫ - π π f x 2018 x + 1 d x bằng
A. 2018
B. 4036
C. 0
D. 1 2018
Trên đoạn - π ; π , hàm số y = sin x có mấy điểm cực trị ?
A. 2
B. 3
C. 4
D. 5
Cho đồ thị hàm số y=1 + cosx (C) và y=1 + cos(x-α) (C') trên đoạn [ 0 ; π ] với 0 < α < π 2 . Tính α biết rằng diện tích hình phẳng giới hạn bởi (C) và (C') và đường x = 0 thì bằng diện tích hình phẳng giới hạn với(C') và đường y = 1, x = π . Ta được kết quả nào sau đây
A. α = π 6
B. α = π 4
C. α = π 3
D. α = π 12
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)=m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi
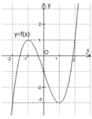
A. m ∈ { - 3 ; 1 } .
B. m ∈ ( - 3 ; 1 )
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]