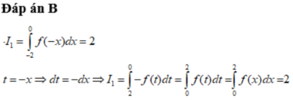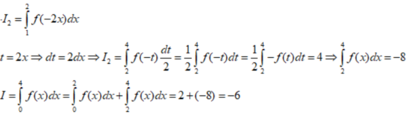Các câu hỏi tương tự
Cho hàm số yf(x) là hàm lẻ, liên tục trên [-4;4], biết
∫
-
2
0
f
(
-
x
)
dx
2
và
∫
1
2
f
(
-
2
x...
Đọc tiếp
Cho hàm số y=f(x) là hàm lẻ, liên tục trên [-4;4], biết ∫ - 2 0 f ( - x ) dx = 2 và ∫ 1 2 f ( - 2 x ) dx = 4 . Tính I= 2 ∫ 0 4 f ( x ) dx
A. I = -10.
B. I = -6.
C. I = 6.
D. I = 10
Cho hàm số y f(x) là hàm lẻ và liên tục trên [-4;4] biết
∫
−
2
0
f
−
x
d
x
2
và
∫
1
2
f
−
2
x
d
x
4
. Tính
I
∫...
Đọc tiếp
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ − 2 0 f − x d x = 2 và ∫ 1 2 f − 2 x d x = 4 . Tính I = ∫ 0 4 f x d x .
A. I = 10
B. I = -6
C. I = 6
D. I = -10
Cho hàm số y f(x) là hàm lẻ và liên tục trên [-4;4] biết
∫
−
2
0
f
−
x
d
x
2
và
∫
1
2
f...
Đọc tiếp
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ − 2 0 f − x d x = 2 và ∫ 1 2 f − 2 x d x = 4. Tính I = ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y f(x) có đạo hàm liên tục trên R đồ thị hàm số y f’(x) như hình vẽ.Biết f(2) –6, f(–4) –10 và hàm số g(x) f(x)+
x
2
2
, g(x) có ba điểm cực trị. Phương trình g(x) 0? A. Có đúng 2 nghiệm B. Vô nghiệm C. Có đúng 3 nghiệm D. Có đúng 4 nghiệm
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
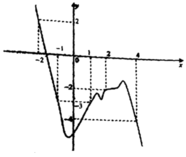
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Cho hàm số y f(x) là hàm lẻ, liên tục trên [-4;4] biết
∫
-
2
0
f
-
x
d
x
2
và
∫
1
2
f
-
2
x
d
x
4
. Tính
∫
0...
Đọc tiếp
Cho hàm số y = f(x) là hàm lẻ, liên tục trên [-4;4] biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số yf(x) có đạo hàm liên tục trên đoạn
[
0
;
2
]
và thỏa mãn
f
(
0
)
2
,
∫
0
2
(
2
x
-
4
)
.
f
(
x
)
d
x
4
. Tính tích phân
I
∫
0...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ] và thỏa mãn f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .
A. I = 2
B. I = - 2
C. I = 6
D. I = - 6
Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng
∫
-
2
0
f
-
x
d
x
2
và
∫
1
2
f
-
2
x
d
x
4
. Tính tích phân
∫
0
4
f...
Đọc tiếp
Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính tích phân ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số yf(x) liên tục trên đoạn
a
;
b
và f(x)0
∀
x
∈
a
;
b
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số yf(x), trục hoành và 2 đường thẳng xa, xb (ab). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
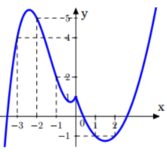
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7