Các câu hỏi tương tự
Cho hàm số y f(x). Hàm số
y
f
x
có đồ thị như hình bên. Biết f(-1) 1,
f
-
1
e
2
. Bất phương trình f(x) ln(-x) + m đúng với mọi
x
∈
-
1
;
-
1
e
...
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
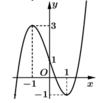
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Cho hàm số y f(x). Hàm số
y
f
x
có đồ thị như hình bên. Biết
f
-
1
1
;
f
-
1
e
2
. Bất phương trình
f
x
ln
-
x
+...
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f - 1 = 1 ; f - 1 e = 2 . Bất phương trình f x < ln - x + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
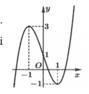
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
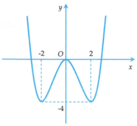
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình bên. Có bao nhiêu số thực m để bất phương trình
m
x
+
m
2
10
-
x
+
3
m
+
1
.
f
(
x
)
≥
0
ng...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Có bao nhiêu số thực m để bất phương trình m x + m 2 10 - x + 3 m + 1 . f ( x ) ≥ 0 nghiệm đúng với mọi x ∈ - 2 ; 3
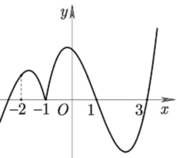
A. 1
B. 3
C. 0
D. 2
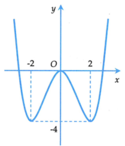
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi A.
m
∈
{
-
3
;
1
}
. B.
m
∈
(
-
3
;
1
)
C.
m
∈
[
-
3
;
1
)
D.
m...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)=m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi
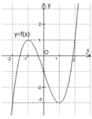
A. m ∈ { - 3 ; 1 } .
B. m ∈ ( - 3 ; 1 )
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Cho hàm số yf(x). Hàm số yf’(x) có đồ thị như hình vẽ:Bất phương trình
f
x
36
+
x
+
3
-
2
x
-
1
m
đúng với mọi mÎ(0;1) khi và chỉ khi A. ...
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ:
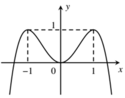
Bất phương trình f x 36 + x + 3 - 2 x - 1 > m đúng với mọi mÎ(0;1) khi và chỉ khi
A. m ≤ f 1 + 9 36
B. m < f 1 + 9 36
C. m > f 1 + 9 36
D. m ≥ f 1 + 9 36
Cho hàm số yf(x) có đạo hàm liên tục trên , đồ thị hàm số yf’(x) như hình vẽ bên dưới. Cho bất phương trình
f
e
x
+
2
3
e
3
x
-
e
x
-
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
e...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2
Cho hàm số yf(x) xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Gọi m là số nghiệm thực của phương trình f(f(x))0 Khẳng định nào sau đây là đúng? A. m5 B. m6 C. m7 D. m8
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R. Đồ thị của hàm số f(x) như hình bên. Gọi m là số nghiệm thực của phương trình f(f(x))=0 Khẳng định nào sau đây là đúng?

A. m=5
B. m=6
C. m=7
D. m=8
Cho hàm số
y
f
(
x
)
xác định và liên tục trên
ℝ
. Đồ thị của hàm số
f
(
x
)
như hình bên. Gọi m là số nghiệm thực của phương trình
f
(
f
(
x
)
)
1
. Khẳng định nào sau đây là đúng? A.
m
5
B.
m
6
C.
m...
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ . Đồ thị của hàm số f ( x ) như hình bên. Gọi m là số nghiệm thực của phương trình f ( f ( x ) ) = 1 . Khẳng định nào sau đây là đúng?
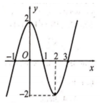
A. m = 5
B. m = 6
C. m = 7
D. m = 9
Cho hàm số y f(x) liên tục trên . Hàm số f’(x) có đồ thị như hình vẽ. Bất phương trình
f
(
2
sinx
)
-
2
sin
2
x
m
đúng với mọi khi và chỉ khi :
A
.
m
f
(
1
)
-
1
2
B
.
m
≥...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên . Hàm số f’(x) có đồ thị như hình vẽ. Bất phương trình f ( 2 sinx ) - 2 sin 2 x < m đúng với mọi khi và chỉ khi :

A . m > f ( 1 ) - 1 2
B . m ≥ f ( 1 ) - 1 2
C . m ≥ f ( 0 ) - 1 2
D . m > f ( 0 ) - 1 2