Đáp án C
Ta có y ' = e x x 2 + m x + 2 x + m e x = e x x 2 m + 2 x + m
y ' 0 = 1 ⇒ m = 1 ⇒ y ' = e x x 2 + 3 x + 1 ⇒ y ' 1 = 5 e
Đáp án C
Ta có y ' = e x x 2 + m x + 2 x + m e x = e x x 2 m + 2 x + m
y ' 0 = 1 ⇒ m = 1 ⇒ y ' = e x x 2 + 3 x + 1 ⇒ y ' 1 = 5 e
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
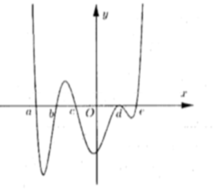
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số y = f(x) có f’ (x) liên tục trên nửa khoảng [0;+∞) thỏa mãn biết 3f(x) + f(x) = 1 + 3 e - 2 x . Giá trị f(0) = 11 3 . Giá trị f 1 2 ln 6 bằng
A. 1 2
B. 5 6 18
C. 1
D. 5 6 9
Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x2+2x)e-f(x) ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1)
![]()
![]()
![]()
![]()
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
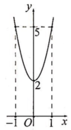
A. 30
B. 24
C. 26
D. 27
Cho hàm số y=f(x) có đạo hàm liên tục trên (1;+∞) và thỏa mãn x f ' ( x ) - 2 f ( x ) . l n x = x 3 - f ( x ) ,∀x∈(1;+∞); biết f ( e 3 ) = 3 e . Giá trị f(2) thuộc khoảng nào dưới đây
A. ( 12 ; 25 / 2 )
B. ( 13 ; 27 / 2 )
C. ( 23 / 2 ; 12 )
D. ( 14 ; 29 / 2 )
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Cho hàm số y = x + b a x − 2 a b ≠ − 2 . Biết rằng a v à b là các giá tri thoả mãn tiếp tuyến của đồ thị hàm số tại điểm M 1 ; − 2 song song với đường thẳng d : 3 x + y − 4 = 0. Khi đó giá trị của bằng
A.2
B.0
C.-1
D.1