Các câu hỏi tương tự
Cho hàm số
y
a
x
−
b
b
x
+
1
có đồ thị (C). Nếu (C) có tiệm cận ngang là đường thẳng y2 và tiệm cận đứng là đường thẳng
x
1
3
thì các giá trị của a và b lần lượt là : A.
−
1
2...
Đọc tiếp
Cho hàm số y = a x − b b x + 1 có đồ thị (C). Nếu (C) có tiệm cận ngang là đường thẳng y=2 và tiệm cận đứng là đường thẳng x = 1 3 thì các giá trị của a và b lần lượt là :
A. − 1 2 và − 1 6
B. -3 và -6
C. − 1 6 và − 1 2
D. -6 và -3
Tìm số phát biểu đúng trong các phát biểu sau:(1) Đồ thị hàm số y
x
α
với
α
0
nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.(2) Đồ thị hàm số y
x
α
với
α
0
không có tiệm cận.(3) Đồ thị hàm số
y
log
a
x
với
1
a...
Đọc tiếp
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Biết rằng các đường thẳng x1,y2 lần lượt là đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
2
a
x
+
1
x
-
b
Tính giá trị Ta+b+ab A. T4. B. T0. C. T2. D. T3.
Đọc tiếp
Biết rằng các đường thẳng x=1,y=2 lần lượt là đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 a x + 1 x - b Tính giá trị T=a+b+ab
A. T=4.
B. T=0.
C. T=2.
D. T=3.
Tất cả các giá trị thực của tham số m để đường thẳng
d
:
y
2
x
+
m
cắt đồ thị hàm số
y
2
x
-
4
x
-
1
tại hai điểm phân biệt A và B sao cho
4
S
∆
I
A...
Đọc tiếp
Tất cả các giá trị thực của tham số m để đường thẳng d : y = 2 x + m cắt đồ thị hàm số y = 2 x - 4 x - 1 tại hai điểm phân biệt A và B sao cho 4 S ∆ I A B = 15 , với I là giao điểm của hai đường tiệm cận của đồ thị (C) là
A. m = ± 5
B. m = 0
C. m = 5
D. m = - 5
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số
y
2
x
+
1
x
+
1
(C), gọi I là tâm đối xứng của đồ thị (C) và M(a;b) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị (C) tại điểm M cắt hai tiệm cận của đồ thị (C) lần lượt tại hai điểm A và B. Để tam giác IAB có bán kính đường tròn nội tiếp lớn nhất thì tổng a+b gần nhất với số nào sau đây? A. -3. B. 0. C. 3...
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 (C), gọi I là tâm đối xứng của đồ thị (C) và M(a;b) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị (C) tại điểm M cắt hai tiệm cận của đồ thị (C) lần lượt tại hai điểm A và B. Để tam giác IAB có bán kính đường tròn nội tiếp lớn nhất thì tổng a+b gần nhất với số nào sau đây?
A. -3.
B. 0.
C. 3.
D. 5.
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai? A. M là trung điểm của AB B. Diện tích tam giác IAB là một số không đổi C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi D. Tổng khoảng cách từ M đến hai tiệm cận là mộ...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai?
A. M là trung điểm của AB
B. Diện tích tam giác IAB là một số không đổi
C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi
D. Tổng khoảng cách từ M đến hai tiệm cận là một số không đổi
Cho các số thực dương a, b khác 1. Biết rằng đường thẳng y2 cắt đồ thị của các hàm số
y
a
x
,
y
b
x
và trục tung lần lượt tại A, B và C sao cho C nằm giữa A và B và AC2BC. Khẳng định nào dưới đây đúng A. b
a
2
B. b2a C. b
a
-
2
D. b...
Đọc tiếp
Cho các số thực dương a, b khác 1. Biết rằng đường thẳng y=2 cắt đồ thị của các hàm số y = a x , y = b x và trục tung lần lượt tại A, B và C sao cho C nằm giữa A và B và AC=2BC. Khẳng định nào dưới đây đúng
A. b= a 2
B. b=2a
C. b= a - 2
D. b= a 2
Cho hàm số
y
x
+
1
x
-
1
có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng A. 16. B. 32. C. 8. D. 4.
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng
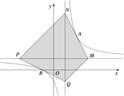
A. 16.
B. 32.
C. 8.
D. 4.




